题目内容
5.(1)计算:($\frac{1}{3}$)-1-|-2|+$\sqrt{16}$-($\sqrt{3}$+1)0;(2)化简:$\frac{ab+c}{a+b}+\frac{{{a^2}-c}}{a+b}$.
分析 (1)根据负整数指数幂、零指数幂的法则、算术平方根的定义、绝对值的性质进行计算即可;
(2)根据分式的混合运算法则计算.
解答 解:(1)原式=3-2+4-1
=4;
(2)原式=$\frac{{ab+{a^2}}}{a+b}$
=$\frac{a(b+a)}{a+b}$
=a.
点评 本题考查的是负整数指数幂、零指数幂、算术平方根、绝对值和分式的混合运算,掌握负整数指数幂、零指数幂的法则、算术平方根的定义、绝对值的性质以及分式的混合运算法则是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
15.下列说法错误的是( )
| A. | 相等的角是对顶角 | |
| B. | 同角的补角相等 | |
| C. | 直线外一点与直线上各点连接的所有线段中,垂线段最短 | |
| D. | 平行于同一条直线的两条直线平行 |
16.下列各式子中,是二元一次方程的是( )
| A. | x+2y=3z | B. | xy=1 | C. | x+y=1 | D. | x-yz=2008 |
20.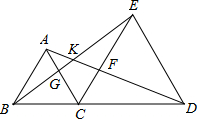 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )
如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )
 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )
如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
14.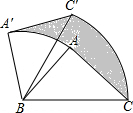 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |

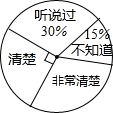 第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.
第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.