题目内容
在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
解:画树状图得:

(1)点Q所有可能的坐标有:
(1, 2),(1,3),(1,4)
(2,1),(2,3),(2,4)
(3,1),(3,2),(3,4)
(4,1),(4,2),(4,3)
共12种.
(2)∵共有12种等可能的结果,其中在函数y=﹣x+5的图象上的有4种,即:
(1,4),(2,3),(3,2),(4,1),
∴点(x,y)在函数y=﹣x+5的图象上的概率为: =
= .
.
(3)∵x、y满足xy>6有:(2,4),(3,4),(4,2),(4,3)共4种情况,x、y满足xy<6有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1)共6种情况.
 ,
,
 . 公平的游戏规则为:若
. 公平的游戏规则为:若 、
、 满足
满足 则小明胜,
则小明胜,
若 、
、 满足
满足 <6则小红胜.
<6则小红胜.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形 的面积之和为_________cm2.
的面积之和为_________cm2. 有意义,则
有意义,则 的取值范围是
的取值范围是 B.
B. C.
C. ,
, 在二次函数
在二次函数 的图象上,若
的图象上,若 ,则
,则 (填“>”、“=”或“<”).
(填“>”、“=”或“<”). 与点
与点 重合,点N到达点
重合,点N到达点 时运动终止),过点M、N分别作
时运动终止),过点M、N分别作 边的垂线,与△ABC的其他边交于P、Q两点,线段MN运动的时间为
边的垂线,与△ABC的其他边交于P、Q两点,线段MN运动的时间为 秒.
秒.
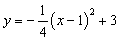 与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.点P在抛物线上,直线PQ//BC交x轴于点Q,连接BQ.
与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.点P在抛物线上,直线PQ//BC交x轴于点Q,连接BQ.