题目内容
如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于G、H.
⑴求证:△ABE∽△ADF;
⑵若AG=AH,求证:四边形ABCD是菱形.

证明:⑴∵AE⊥BC,AF⊥CD ∴∠AEB=∠AFD=90
∵四边形ABCD是平行四边∴∠ABE=∠ADF.
∴△ABE≌△ADF.
(2)∵△ABE∽△ADF,
∴∠BAG=∠DAH.
∵AG=AH,∴∠AGH=∠AHG,
从而∠AGB=∠AHD.
∴△ABG≌△ADH.
∴ .
.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.

练习册系列答案
相关题目
某中学为了让学生的跳远在中考体育测试中取得满意的成绩,在锻炼一个月后,学校对九年级一班的45名学生进行测试,成绩如下表:
| 跳远成绩(cm) | 160 | 170 | 180 | 190 | 200 | 220 |
| 人数 | 3 | 9 | 6 | 9 | 15 | 3 |
这些运动员跳远成绩的中位数和众数分别是______
A. 190,200 B.9,9 C.15,9 D.185,200
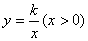 的图象经过点A.若S△BEC=4,则k的值
的图象经过点A.若S△BEC=4,则k的值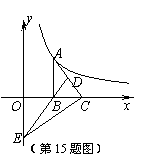 为 ;
为 ;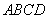 中,
中, ,
,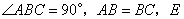 为
为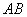 边上一点,
边上一点, ,且
,且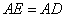 .连接
.连接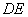 交对角线
交对角线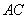 于
于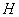 ,连接
,连接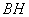 .下列结论:
.下列结论: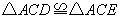 ;②
;②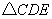 为等边三角形;③
为等边三角形;③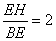 ; ④.
; ④.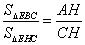
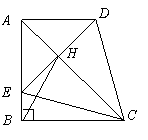
 的图象上的两点,过点M作直线MB∥x轴,交
的图象上的两点,过点M作直线MB∥x轴,交 轴于点B;过点
轴于点B;过点 作直线
作直线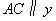 轴交
轴交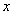 轴于点
轴于点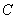 ,交直线MB于点D.BM:DM=8:9,当四边形OADM的面积为
,交直线MB于点D.BM:DM=8:9,当四边形OADM的面积为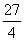 时,k= .
时,k= .  的平均数是5,则另一组新数组
的平均数是5,则另一组新数组 的平均数是( )
的平均数是( ) 中,
中,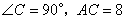 ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持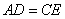 .连接DE、DF、EF.在此运动变化的过程中,下列结论:①
.连接DE、DF、EF.在此运动变化的过程中,下列结论:①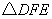 是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是( )
是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是( )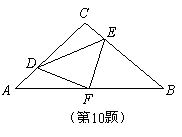


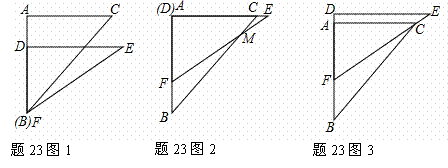
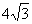 ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。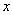 ,两块三角板重叠部分面积为
,两块三角板重叠部分面积为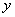 ,求
,求