题目内容
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为( )
A.5+

B.4

C.3+2

D.4+

【答案】分析:根据旋转的性质,得BC=DE=5,BE=AC=3,则CE=8;根据旋转的性质可知△COE是等腰直角三角形,计算可得OC的长.
解答:解:根据旋转的性质,得BC=DE=5,BE=AC=3,则CE=8,
根据旋转的性质,知△COE是等腰直角三角形,则OC=OE=4 .
.
故选B.
点评:熟悉旋转的性质,根据旋转的两个图形全等,得到对应边相等,根据旋转角得到直角三角形,再进一步根据勾股定理计算.
解答:解:根据旋转的性质,得BC=DE=5,BE=AC=3,则CE=8,
根据旋转的性质,知△COE是等腰直角三角形,则OC=OE=4
 .
.故选B.
点评:熟悉旋转的性质,根据旋转的两个图形全等,得到对应边相等,根据旋转角得到直角三角形,再进一步根据勾股定理计算.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
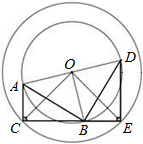 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为( )
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为( )A、5+
| ||||
B、4
| ||||
C、3+2
| ||||
D、4+
|
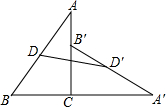 如图将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,已知AC=12cm,BC=5cm,则线段DD′的长为
如图将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,已知AC=12cm,BC=5cm,则线段DD′的长为 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为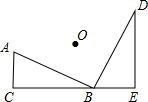 如图,Rt△ABC绕O点逆时针旋转90°得Rt△BDE,其中∠ABD=∠ACB=∠BED=90°,AC=3,DE=5,则OC的长为( )
如图,Rt△ABC绕O点逆时针旋转90°得Rt△BDE,其中∠ABD=∠ACB=∠BED=90°,AC=3,DE=5,则OC的长为( )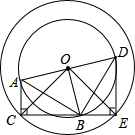 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则DB的长为( )
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则DB的长为( )