题目内容
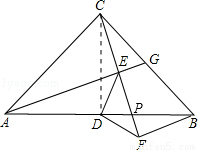
已知等腰Rt△ABC中,∠ACB=90°,AC=BC,点G在BC上,连接AG,过C作CF⊥AG,垂足为点E,过点B作BF⊥CF于点F,点D是AB的中点,连接DE、DF
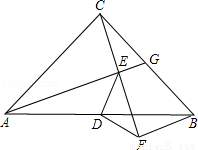
(1)若∠CAG=30°,EG=1,求BG的长;
(2)求证:∠AED=∠DFE.
(1)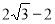 ;(2)证明见试题解析.
;(2)证明见试题解析.
【解析】
试题分析:(1)首先根据勾股定理求出CE的长,进而得到AC的长,因为AC=BC,所以BC可求,利用BH=BC﹣CG计算即可;
(2)连接CD,通过证明分别证明△ACE≌△CBF和△DCE≌△DBF,利用全等三角形的性质即可证明∠AED=∠DFE.
解答:(1)【解析】
∵∠ACE=∠ECG=30°,EG=1,sin30°=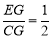 ,∴CG=2,∴CE=
,∴CG=2,∴CE=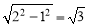 ,
,
∵sin30°=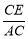 ,∴AC=
,∴AC= ,∴BC=
,∴BC= ,∴BG=
,∴BG=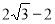 ;
;
(2)证明:连接CD,
在△ACE和△CBF中,∵∠AEC=∠CFB,∠CAE=∠FCB,AC=BC,∴△ACE≌△CBF(AAS),∴CE=BF,
∵等腰RT△ABC中,点D是AB的中点,∴CD=BD,
∵CD⊥BD,∠DCE+∠DPC=∠FBP+∠FPB=90°,∴∠DCE=∠DBF,
在△DCE和△DBF中,
∵CF=BF,∠DCE=∠DBF,DC=BD,∴△DCE≌△DBF(SAS),∴∠CED=∠BFD,
∵∠AEC=∠CFB=90°,∴∠AED=∠DFE.
考点:1.全等三角形的判定与性质;2.等腰直角三角形;3.解直角三角形.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 ,
, ,
,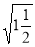 ,
, 中最简二次根式的个数是 ( )
中最简二次根式的个数是 ( ) 与x轴、y轴分别交于点A、B,已知点P是第一象限内的点,由点P、O、B组成了一个含60°的直角三角形,则点P的坐标为 .
与x轴、y轴分别交于点A、B,已知点P是第一象限内的点,由点P、O、B组成了一个含60°的直角三角形,则点P的坐标为 .
 的根是( )
的根是( ) B.
B. C.
C. D.
D.


 =
= D.
D. =
=
 经过直角三角形
经过直角三角形 斜边
斜边 的中点
的中点 ,与直角边
,与直角边 相交于点
相交于点 .过
.过 作
作 ⊥
⊥ 交
交 于点
于点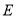 ,若△
,若△ 的面积为
的面积为 ,则
,则 的值是 ( ).
的值是 ( ).
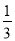 D.
D.
