题目内容
 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是( )A.

B.

C.

D.

【答案】分析:过点A作AD⊥l1于D,过点B作BE⊥l1于E,根据同角的余角相等求出∠CAD=∠BCE,然后利用“角角边”证明△ACD和△CBE全等,根据全等三角形对应边相等可得CD=BE,然后利用勾股定理列式求出AC,再根据等腰直角三角形斜边等于直角边的 倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.
倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.
解答: 解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,
解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,
∵∠CAD+∠ACD=90°,
∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在等腰直角△ABC中,AC=BC,
在△ACD和△CBE中, ,
,
∴△ACD≌△CBE(AAS),
∴CD=BE=1,
在Rt△ACD中,AC= =
= =
= ,
,
在等腰直角△ABC中,AB= AC=
AC= ×
× =
= ,
,
∴sinα= =
= .
.
故选D.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,锐角三角函数的定义,作辅助线构造出全等三角形是解题的关键.
 倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.
倍求出AB,然后利用锐角的正弦等于对边比斜边列式计算即可得解.解答:
 解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,
解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,∵∠CAD+∠ACD=90°,
∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在等腰直角△ABC中,AC=BC,
在△ACD和△CBE中,
 ,
,∴△ACD≌△CBE(AAS),
∴CD=BE=1,
在Rt△ACD中,AC=
 =
= =
= ,
,在等腰直角△ABC中,AB=
 AC=
AC= ×
× =
= ,
,∴sinα=
 =
= .
.故选D.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,锐角三角函数的定义,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
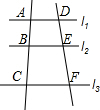 如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=16,则DE=
如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=16,则DE= (2012•甘孜州)如图,已知l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果正方形ABCD的四个顶点分别在四条直线上,AB与l2交于点E,则△AED与正方形ABCD的面积之比为
(2012•甘孜州)如图,已知l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果正方形ABCD的四个顶点分别在四条直线上,AB与l2交于点E,则△AED与正方形ABCD的面积之比为 (2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( )
(2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( ) 如图,已知l1∥l2,∠2=30°,∠3=25°,则∠1的度数是( )
如图,已知l1∥l2,∠2=30°,∠3=25°,则∠1的度数是( ) 如图,已知l1∥l2,∠1=65°,∠2=35°,求∠x和∠y的度数.
如图,已知l1∥l2,∠1=65°,∠2=35°,求∠x和∠y的度数.