Question

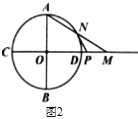
【题目】如图，在□ABCD中，AB＝2cm，线段AB与直线l之间的距离为cm，线段CD的起始位置在MN处，此时∠MAB＝1350，现将线段CD在直线l上向右移动，移动速度为1cm/s，运动时间为ts．

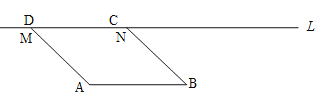
（1）当t＝____s时，□ABCD为矩形；

（2）线段CD在直线l上移动过程中，当□ABCD为菱形时，求线段CD运动时间t的值．

Answer 1

【答案】（1）；（2）t=－1或＋1.

【解析】

（1）根据矩形和等腰三角形的性质得到MD=AD，故可求解；

（2）根据题意可分两种情况作图，再根据菱形的性质与勾股定理进行求解.

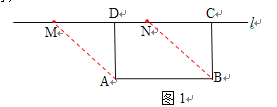
解（1）如图1，根据矩形的性质可知∠DAB=∠ADC=90°，故∠ADM=45°，又AD=,∴MD=，

故当t＝时，□ABCD为矩形；

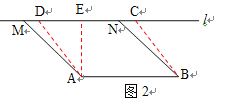
（2）①如图2，过A作AE⊥MN

当四边形ABCD为菱形时，

∴AD＝AB＝2

在Rt△ADE中

DE＝＝1

在Rt△AME中

∠MAE＝1350－900＝450

∴ME＝AE＝

MD＝－1

t＝－1

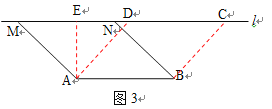
②如图3，过A作AE⊥MN

当四边形ABCD为菱形时，

∴AD＝AB＝2

由①易得

DE＝1， ME＝

MD＝＋1

t＝＋1

∴线段运动－1或＋1秒时，四边形ABCD为菱形