题目内容
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;0≤x≤
;0≤x≤![]() .
.
【解析】试题分析:(1)由正方形的性质及![]() 可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△
可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△![]() ∽△
∽△![]() 即可求出结论;
即可求出结论;
(2)由正方形的性质得∠A=∠ABC=∠C=90°,由MQ∥AB得∠QMR=∠A,故∠QMR=∠C;由MQ∥AB得![]() ,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故
,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故![]() ,从而△
,从而△![]() ∽△
∽△![]() .故可得出结论;
.故可得出结论;
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,通过证明
,通过证明![]() ,分别计算
,分别计算![]() 及
及![]() ,
, ![]() ,从而可得出结论.
,从而可得出结论.
试题解析:(1)由题意,得![]() ,
,![]()
在Rt△![]() 中,
中, ![]()
∴![]()
∵![]()
∴![]() ∴
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴△![]() ∽△
∽△![]()
∴![]()
∴![]()
∴![]()
(2)答: ![]() 的比值随点
的比值随点![]() 的运动没有变化
的运动没有变化
理由:如图,
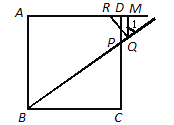
∵![]() ∥
∥![]()
∴![]() ,
, ![]()
∵![]()
∴![]()
∵![]()
∴![]()
![]()
∴![]()
∴△![]() ∽△
∽△![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∴![]() 的比值随点
的比值随点![]() 的运动没有变化,比值为
的运动没有变化,比值为![]()
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]()
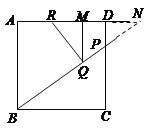
∵![]() ∥
∥![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ∥
∥![]() ,
, ![]() ∥
∥![]()
∴![]() ∥
∥![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
又![]() ,
, ![]()
∴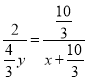
∴![]()
它的定义域是![]()

练习册系列答案
相关题目








