题目内容
14. 如图,直线l1∥l2,等腰Rt△ABC的直角顶点C在l1上,顶点A在l2上,若∠β=14°,则∠α=( )
如图,直线l1∥l2,等腰Rt△ABC的直角顶点C在l1上,顶点A在l2上,若∠β=14°,则∠α=( )| A. | 31° | B. | 45° | C. | 30° | D. | 59° |
分析 首先过点B作BE∥l1,可得BE∥l1∥l2,然后根据两直线平行,内错角相等,即可求得答案.
解答  解:过点B作BE∥l1,
解:过点B作BE∥l1,
∵l1∥l2,
∴BE∥l1∥l2,
∴∠CBE=∠α,∠EBA=∠β=14°,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∴∠α=∠CBE=∠ABC-∠EBA=31°.
故选:A.
点评 此题考查了平行线的性质.此题比较简单,注意掌握辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5.某校八年级参加春季植树活动,各班参加活动的人数统计如下57,61,53,61,59,51,对于这组统计数据,下列说法中正确的是( )
| A. | 众数是61 | B. | 中位数为57 | C. | 极差是39 | D. | 平均数为58 |
2.一次函数y=-$\frac{3}{2}$x-1的图象不经过的象限是( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
3.下列算式计算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{121÷4}$=$\sqrt{121}$÷$\sqrt{4}$=$\frac{11}{2}$ |
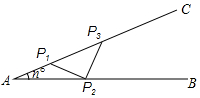 如图钢架中,∠A=14°,依次焊上等长的钢条P1P2,P2P3,…,来加固钢架,这样的钢条最多能焊( )根.
如图钢架中,∠A=14°,依次焊上等长的钢条P1P2,P2P3,…,来加固钢架,这样的钢条最多能焊( )根. 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).下列结论: 如图,AB∥CD∥EF,如果AC=2,AE=6,DF=3,那么BD=1.5.
如图,AB∥CD∥EF,如果AC=2,AE=6,DF=3,那么BD=1.5.