题目内容
4. 如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4.
如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4.(1)求反比例函数的解析式及交点A、B的坐标;
(2)直接写出不等式$\frac{k}{x}$>2x的解集;
(3)若P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,请直接写出满足条件的P点坐标.
分析 (1)利用△AOE的面积可求得k=OE•AE,再由两函数解析式可求得A、B坐标;
(2)由$\frac{k}{x}$>2x可知反比例函数图象在正比例函数图象的上方,结合A、B坐标可写出不等式的解集;
(3)可求得OE的长,分P点在x轴下方和P在x轴上方两种情况,再结合平行四边形的性质可分别求得P点坐标.
解答 解:(1)如图1,
∵△AOE的面积为4,函数y=$\frac{k}{x}$的图象过一、三象限,
∴S△AOE=$\frac{1}{2}$•OE•AE=4,
∴OE•AE=8,
∴xy=8,
∴k=8,
∴反比例函数解析式为y=$\frac{8}{x}$
∵函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,
∴2x=$\frac{8}{x}$,
∴x=±2,
当x=2时,y=4,当x=-2时,y=-4,
∴A、B两点的坐标是:(2,4)(-2,-4);
(2)当$\frac{k}{x}$>2x时,即反比例函数图象在正比例函数图象的上方,
由图象可知x的取值范围为x<-2或0<x<2,
∴不等式$\frac{k}{x}$>2x的解集为x<-2或0<x<2;
(3)由(1)可求得E点坐标为(2,0),∴OE=2,如图2,
当P点在x轴下方时,则有BP∥OE且BP=OE=2,且B点坐标为(-2,-4),
∴P点坐标分别为(0,-4)或(-4,-4),
当P点在x轴上方时,则有BO∥PE,且P到x轴的距离和B到x轴的距离相等,可求得此时P点坐标为(4,4),
综上可知满足条件的P点有3个,分别为:P1(0,-4),P2(-4,-4),P3(4,4).
点评 本题主要考查反比例函数综合应用,涉及待定系数法、图象的交点坐标、反比例函数的性质和平行四边形的性质等知识点.在(1)中注意k=xy的应用,在(2)中注意数形结合的应用,在(3)中确定出P的位置是解题的关键.本题考查知识相对基础,难度不大.

 名校课堂系列答案
名校课堂系列答案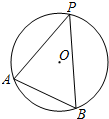 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
| 甲 | 10 | 9 | 8 | 5 | 8 |
| 乙 | 8 | 8 | 7 | 9 | 8 |
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$<${s_乙}^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2={s_乙}^2$ | D. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ |
| A. | 5×107 | B. | 50×106 | C. | 5×106 | D. | 0.5×108 |
| 地区类别 | 首小时内 | 首小时外 | 备注 |
| A类 | 1.5元/15分钟 | 2.75元/15分钟 | 不足15分钟时 按15分钟收费 |
| B类 | 1.0元/15分钟 | 1.25元/15分钟 | |
| C类 | 免费 | 0.75元/15分钟 |
| A. | 5 | B. | -5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |

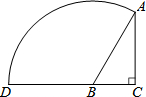 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$.
如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$.