题目内容
11.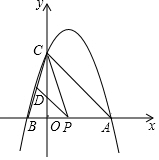 如图,已知二次函数y=ax2+bx+4的图象经过点A(4,0)、B(-2,0).
如图,已知二次函数y=ax2+bx+4的图象经过点A(4,0)、B(-2,0).(1)直接写出C点坐标;
(2)求此二次函数的表达式;
(3)连结AC、BC,P是线段AB上的一动点(P不与A、B重合),过P作PD∥AC,交BC于D,连结CP当P在什么位置时,△PCD的面积取最大值?求出这个最大值.
分析 (1)根据抛物线的解析式求得点C的坐标;
(2)把点A、B的坐标分别代入函数解析式,利用待定系数法求得该抛物线的解析式即可;
(3)设点P的坐标为(m,0),利用相似三角形的判定定理推知△PBD∽△ABC,结合相似三角形的性质易推知△PBD的边PB上的高为h=$\frac{2}{3}$(m+2).根据图形得到S△PCD=S△PBC-S△PBD,利用二次函数最值的求法进行解答即可.
解答  解:(1)∵抛物线的解析式是y=ax2+bx+4,
解:(1)∵抛物线的解析式是y=ax2+bx+4,
∴当x=0时,y=4,
∴C(0,4);
(2)把A(4,0)、B(-2,0)代入y=ax2+bx+4,得
$\left\{\begin{array}{l}{16a+4b+4=0}\\{4a-2b+4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
故该函数解析式为:y=-$\frac{1}{2}$x2+x+4;
(3)设点P的坐标为(m,0),则-2<m<4,PB=m+2,AB=6,
∵PD∥AC,
∴△PBD∽△ABC,
设△PBD的边PB上的高为h,
∴$\frac{BP}{BA}$=$\frac{h}{OC}$,即h=$\frac{2}{3}$(m+2).
∴S△PCD=S△PBC-S△PBD=$\frac{1}{2}$(m+2)×4-$\frac{1}{2}$(m+2)($\frac{2}{3}$m+2).即S△PCD=-$\frac{1}{3}$(m-1)2+3.
当m=1时,△PCD的面积取最大值3,此时点P的坐标为(1,0).
点评 本题考查了二次函数综合题,需要系统掌握二次函数图象上点的坐标特征,待定系数法求二次函数的解析式,三角形面积的求法以及二次函数最值的求法,难度较大.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | 内错角相等 | |
| B. | 两角及一边对应相等的两个三角形全等 | |
| C. | 1的立方根是±1 | |
| D. | -1是无理数 |