Question

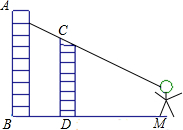身高1.7米的小明站在平坦的公路上，见前方有AB，CD两建筑物，这时还能从CD的上端见到AB的一部分，且他的视线与水平线的夹角α=30°，已知CD=16.7米高，若小明继续向前走到N的位置时，AB刚好被CD遮住，此时他的视线与水平线的夹角β=45°，则小明从M向N行进了

（15

3

-15）

米．

Answer 1

分析：将题目中的已知条件总结为CD=16.7，HM=GN=1.7，∠CHE=30°，∠CGE=45°，然后在两个直角三角形中求得DM和DN的长，相减即可求得MN的值．

解答：解：如图，由已知得：CD=16.7，HM=GN=1.7，∠CHE=30°，∠CGE=45°，
∴CE=CD-HM=16.7-1.7=15米，
∴EH=DM=

CE

tan30°

=

15

3 3

=15

3

m
在Rt△CEG中，
∵∠CGE=45°，
∴EG=DN=CE=15m
∴MN=DM-DN=15

3

-15
∴小明从M向N行进了（15

3

-15）米，
故答案为：（15

3

-15）

点评：本题考查了解直角三角形的应用，解题的关键是从复杂的实际问题中整理出直角三角形并求解．