题目内容
某厂成功研制出一种市场需求量较大的高科技产品,已知生产每件产品的成本为60元,在销售过程中发现:当销售单价为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x元,年销售量为y万件,年利润为z万元.
(1)写出y与x之间的函数关系式;
(2)写出z与x之间的函数关系式;
(3)销售单价为多少时,年利润最大?最大年利润是多少?
(1)写出y与x之间的函数关系式;
(2)写出z与x之间的函数关系式;
(3)销售单价为多少时,年利润最大?最大年利润是多少?
考点:二次函数的应用
专题:销售问题
分析:(1)由销售单价为x元,可得销售单价增加量,年销售量减少量,实际销售量,即可得出y与x之间的函数关系式,
(2)当销售单价为x元时,每件销售利润为(x-60)元,销售量为-
+30万件,可得z与x之间的函数关系式;
(3)由z与x之间的函数关系式;即可求出年利润最大值.
(2)当销售单价为x元时,每件销售利润为(x-60)元,销售量为-
| x |
| 10 |
(3)由z与x之间的函数关系式;即可求出年利润最大值.
解答:解:(1)∵当销售单价为x元(x>100)时,销售单价增加了(x-100)元,年销售量减少了
万件,实际销售量为(20-
)万件,
∴y=20-
=-
+30
即y=-
+30,
(2)∵当销售单价为x元时,每件销售利润为(x-60)元,销售量为-
+30万件,
∴z=(x-60)(-
+30),即z=-
+36x-1800
(3)z=-
+36x-1800=-
(x-180)2+1440,
当x=180时,年利润z有最大值,最大年利润是1440万元.
| x-100 |
| 10 |
| x-100 |
| 10 |
∴y=20-
| x-100 |
| 10 |
| x |
| 10 |
即y=-
| x |
| 10 |
(2)∵当销售单价为x元时,每件销售利润为(x-60)元,销售量为-
| x |
| 10 |
∴z=(x-60)(-
| x |
| 10 |
| x2 |
| 10 |
(3)z=-
| x2 |
| 10 |
| 1 |
| 10 |
当x=180时,年利润z有最大值,最大年利润是1440万元.
点评:本题主要考查了二次函数解决利润问题,解题的关键是确定出二次函数的解析式.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 若AB∥CD,∠AEH=130°,那么∠EHC等于多少度( )
若AB∥CD,∠AEH=130°,那么∠EHC等于多少度( )| A、60° | B、70° |
| C、65° | D、50° |

 已知,如图,△ABC中,∠BAC=90°,AB=AC,BD是AC边上的中线,AH⊥BD于H,与BC交于点E,FC⊥AC交AE的延长线于F.
已知,如图,△ABC中,∠BAC=90°,AB=AC,BD是AC边上的中线,AH⊥BD于H,与BC交于点E,FC⊥AC交AE的延长线于F.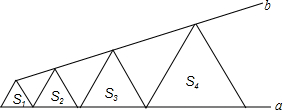 如图,若干个正三角形的一边在同一条直线a上,这边对的顶点也在同一条直线b上,它们的面积依次为S1,S2,S3,S4…若S1=1,S2=2,则S6等于( )
如图,若干个正三角形的一边在同一条直线a上,这边对的顶点也在同一条直线b上,它们的面积依次为S1,S2,S3,S4…若S1=1,S2=2,则S6等于( )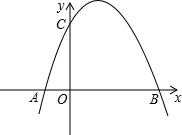 如图,抛物线y=ax2+bx-3a经过A(-1,0)、C(0,3)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-3a经过A(-1,0)、C(0,3)两点,与x轴交于另一点B.