题目内容
 如图,在平面直角坐标系中,点A的坐标为(3,2),直线l的解析式为y=x+1,l与x、y轴分别交于点B、C.
如图,在平面直角坐标系中,点A的坐标为(3,2),直线l的解析式为y=x+1,l与x、y轴分别交于点B、C.(1)求点C的坐标;
(2)求cos∠CBO的值;
(3)在第一象限内,直线l上是否存在点P,使∠OPA=90°?若存在,求出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)把点C的横坐标代入直线方程,即可求得点C的纵坐标,则C(0,1);
(2)将点B的纵坐标代入直线方程即可求得点B的坐标是(-1,0),则易证△BCO的等腰直角三角形,所以根据特殊角的三角形函数值求得cos∠CBO的值;
(3)假设存在P(m,m+1),使∠OPA=90°.则由勾股定理知OP2+PA2=OA2,利用两点间的距离公式即可列出关于m的方程,通过解方程求得点m的值.
(2)将点B的纵坐标代入直线方程即可求得点B的坐标是(-1,0),则易证△BCO的等腰直角三角形,所以根据特殊角的三角形函数值求得cos∠CBO的值;
(3)假设存在P(m,m+1),使∠OPA=90°.则由勾股定理知OP2+PA2=OA2,利用两点间的距离公式即可列出关于m的方程,通过解方程求得点m的值.
解答: 解:(1)令x=0,则y=1,则C(0,1);
解:(1)令x=0,则y=1,则C(0,1);
(2)令y=0,则0=x+1,
解得,x=-1,
∴B(-1,0),
∴OB=1.
∵由(1)知,C(0,1),
∴OC=1,
∴OB=OC.
∴如图,△OBC是等腰直角三角形,
∴∠CBO=45°,
∴cos∠CBO=
;
(3)假设存在点P,使∠OPA=90°.
∵点P在直线y=x+1上,∴设P(m,m+1)(m>0),
∴在直角△OPA中,根据勾股定理知OP2+PA2=OA2,即m2+(m+1)2+(m-3)2+(m+1-2)2=22+32
解得,m=
或m=
(不合题意,舍去),
∴存在这样的点P,其坐标是(
,
).
 解:(1)令x=0,则y=1,则C(0,1);
解:(1)令x=0,则y=1,则C(0,1);(2)令y=0,则0=x+1,
解得,x=-1,
∴B(-1,0),
∴OB=1.
∵由(1)知,C(0,1),
∴OC=1,
∴OB=OC.
∴如图,△OBC是等腰直角三角形,
∴∠CBO=45°,
∴cos∠CBO=
| ||
| 2 |
(3)假设存在点P,使∠OPA=90°.
∵点P在直线y=x+1上,∴设P(m,m+1)(m>0),
∴在直角△OPA中,根据勾股定理知OP2+PA2=OA2,即m2+(m+1)2+(m-3)2+(m+1-2)2=22+32
解得,m=
-3+
| ||
| 4 |
-3-
| ||
| 4 |
∴存在这样的点P,其坐标是(
-3+
| ||
| 4 |
1+
| ||
| 4 |
点评:本题考查了一次函数综合题.其中涉及到的知识点有:一次函数图象上点的坐标特征,两点间的距离公式,勾股定理的应用等.解答(2)题时,也可以根据锐角三角函数的定义进行解答.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
下列各图中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )
如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )| A、26cm2 |
| B、39cm2 |
| C、13cm2 |
| D、52cm2 |
化简:(2x-3y)-(4x-5y)的结果是( )
| A、-2x+2y |
| B、6x+2y |
| C、-2x-8y |
| D、6x-8y |
 如图直线y=-5x+5与坐标轴交于A,B两点,AB的垂直平分线与y=x交于P点,双曲线y=
如图直线y=-5x+5与坐标轴交于A,B两点,AB的垂直平分线与y=x交于P点,双曲线y=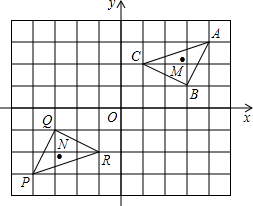 如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下:
如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下: 如图,一张长29cm、宽21cm的长方形纸片,将其中阴影部分裁去后,剩下的部分恰好能沿虚线折叠成一个体积为240cm3的长方体,则该长方体的表面积为
如图,一张长29cm、宽21cm的长方形纸片,将其中阴影部分裁去后,剩下的部分恰好能沿虚线折叠成一个体积为240cm3的长方体,则该长方体的表面积为