题目内容
20.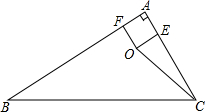 如图,Rt△ABC中,∠BAC=90°,AB=4,BC=5,三角形内有一点O,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且$\frac{AB}{OF}$+$\frac{AC}{OE}$+$\frac{BC}{OD}$=12,求:OD、OE、OF的长.
如图,Rt△ABC中,∠BAC=90°,AB=4,BC=5,三角形内有一点O,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且$\frac{AB}{OF}$+$\frac{AC}{OE}$+$\frac{BC}{OD}$=12,求:OD、OE、OF的长.
分析 连接OB,OA,根据勾股定理得到AC=3,根据三角形的面积公式得到$\frac{1}{2}$AB•AC=$\frac{1}{2}$AB•OF+$\frac{1}{2}$BC•OD+$\frac{1}{2}$AC•OE=12,整理得4OF+5OD+3OE=12,由已知条件得到$\frac{4}{OF}$+$\frac{3}{OE}$+$\frac{5}{OD}$=12,于是得到只有4OF=$\frac{4}{OF}$,5OD=$\frac{5}{OD}$,3OE=$\frac{3}{OE}$时,上述等式成立,于是得到结论.
解答 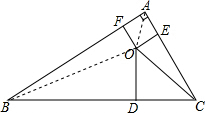 解:连接OB,OA,
解:连接OB,OA,
∵∠BAC=90°,AB=4,BC=5,
∴AC=3,
∵OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,
∴S△ABC=S△ABO+S△BCO+S△ACO,
∴$\frac{1}{2}$AB•AC=$\frac{1}{2}$AB•OF+$\frac{1}{2}$BC•OD+$\frac{1}{2}$AC•OE=12,
∴4OF+5OD+3OE=12,
∵$\frac{AB}{OF}$+$\frac{AC}{OE}$+$\frac{BC}{OD}$=12,
∴$\frac{4}{OF}$+$\frac{3}{OE}$+$\frac{5}{OD}$=12,
∴只有4OF=$\frac{4}{OF}$,5OD=$\frac{5}{OD}$,3OE=$\frac{3}{OE}$时,上述等式成立,
解得:OF=1,OE=1,OD=1.
点评 本题考查了三角形的面积公式,整式的化简,能得出4OF=$\frac{4}{OF}$,5OD=$\frac{5}{OD}$,3OE=$\frac{3}{OE}$是解题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
8.已知:|x|=3,|y|=2,且x>y,则x+y的值为( )
| A. | 5 | B. | 1 | C. | 5或1 | D. | -5或-1 |
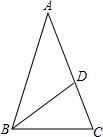 如图,在△ABC中,AB=AC,∠A=36°,点D在边AC上,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,点D在边AC上,BD平分∠ABC.