题目内容
 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为E,连接AC、AD,延长AB交过点C的直线于点P,且∠DCP=∠DAC.
如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为E,连接AC、AD,延长AB交过点C的直线于点P,且∠DCP=∠DAC.(1)求证:PC是⊙O的切线;
(2)若AC=5,CD=6,求PC的长.
考点:切线的判定
专题:证明题
分析:(1)连结OC,根据垂径定理由AB⊥CD得BC弧=BD弧,再根据圆周角定理得∠BOC=∠DAC,而∠DCP=∠DAC,则∠BOC=∠DCP,由于∠ECO+∠EOC=90°,所以∠ECO+∠DCP=90°,于是可根据切线的判定定理得到PC是⊙O的切线;
(2)由AB⊥CD,根据垂径定理得到CE=
CD=3,在Rt△ACE中利用勾股定理计算出AE=4,设⊙O的半径为R,在Rt△OCE中,则OC=R,OE=AE-OA=4-R,
则利用勾股定理得到(4-R)2+32=R2,解得R=
,所以OC=
,OE=4-
=
,然后证明Rt△PCE∽Rt△COE,再利用相似比可计算出PC.
(2)由AB⊥CD,根据垂径定理得到CE=
| 1 |
| 2 |
则利用勾股定理得到(4-R)2+32=R2,解得R=
| 25 |
| 8 |
| 25 |
| 8 |
| 25 |
| 8 |
| 7 |
| 8 |
解答:(1)证明:连结OC,
∵AB⊥CD,
∴BC弧=BD弧,
∴∠BOC=∠DAC,
∵∠DCP=∠DAC,
∴∠BOC=∠DCP,
∵∠ECO+∠EOC=90°,
∴∠ECO+∠DCP=90°,
∴OC⊥PC,
∴PC是⊙O的切线;
(2)∵AB⊥CD,
∴CE=DE=
CD=
×6=3,
在Rt△ACE中,AC=5,CE=3,
∴AE=
=4,
设⊙O的半径为R,
在Rt△OCE中,OC=R,OE=AE-OA=4-R,
∵OE2+CE2=OC2,
∴(4-R)2+32=R2,解得R=
,
∴OC=
,OE=4-
=
,
∵∠EOC=∠DCP,
∴Rt△PCE∽Rt△COE,
∴
=
,即
=
,
∴PC=
.
∵AB⊥CD,
∴BC弧=BD弧,
∴∠BOC=∠DAC,

∵∠DCP=∠DAC,
∴∠BOC=∠DCP,
∵∠ECO+∠EOC=90°,
∴∠ECO+∠DCP=90°,
∴OC⊥PC,
∴PC是⊙O的切线;
(2)∵AB⊥CD,
∴CE=DE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ACE中,AC=5,CE=3,
∴AE=
| AC2-CE2 |
设⊙O的半径为R,
在Rt△OCE中,OC=R,OE=AE-OA=4-R,
∵OE2+CE2=OC2,
∴(4-R)2+32=R2,解得R=
| 25 |
| 8 |
∴OC=
| 25 |
| 8 |
| 25 |
| 8 |
| 7 |
| 8 |
∵∠EOC=∠DCP,
∴Rt△PCE∽Rt△COE,
∴
| PC |
| OC |
| CE |
| OE |
| PC | ||
|
| 3 | ||
|
∴PC=
| 75 |
| 7 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了垂径定理、圆周角定理和相似三角形的判定与性质.

练习册系列答案
相关题目
在同一平面内,从①AB∥CD,②BC∥AD,③AB=CD,④BC=AD.这四个条件中任选两个能使四边形ABCD是平行四边形的选法有( )
| A、3 种 | B、4种 |
| C、5种 | D、6种 |
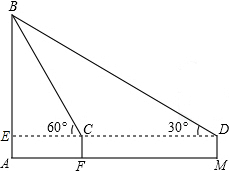 如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取
如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取
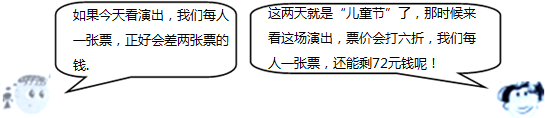
 如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.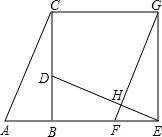 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.