题目内容
已知二次函数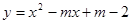 .
.
【小题1】求证:无论m为任何实数,该二次函数的图象与x轴都有两个交点;
【小题2】当该二次函数的图象经过点(3,6)时,求二次函数的解析式;
【小题3】将直线y=x向下平移2个单位长度后与(2)中的抛物线交于A、B两点(点A在点B的左边),一个动点P自A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.求使点P运动的总路径最短的点E、点F的坐标,并求出这个最短总路径的长.
【小题1】证明:令y=0,则 .
.
∵△
 =
= ,
,
又∵ , ∴
, ∴ .即△>0.
.即△>0.
∴无论m为任何实数,一元二次方程 总有两不等实根.
总有两不等实根.
∴该二次函数图象与x轴都有两个交点.
【小题2】解:∵二次函数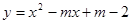 的图象经过点(3,6),
的图象经过点(3,6),
∴ .解得
.解得 .
.
∴二次函数的解析式为
【小题3】解:将 向下平移2个单位长度后得到解析式为:
向下平移2个单位长度后得到解析式为:
解方程组 得
得

∴直线 与抛物线
与抛物线 的交点为
的交点为
∴点A关于对称轴 的对称点是
的对称点是 ,点B关于x轴的对称点是
,点B关于x轴的对称点是 .
. 设过点
设过点 、
、 的直线解析式为
的直线解析式为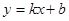 .
.
∴ 解得
解得
∴直线 的解析式为
的解析式为 .
.
∴直线 与x轴的交点为
与x轴的交点为 .
.
与直线 的交点为
的交点为 .
.
则点 、
、 为所求.
为所求.
过点 做
做 ,∴
,∴ ,
, .
.
在Rt△ 中,
中, .
.
∴所求最短总路径的长为
 .
.
解析

练习册系列答案
相关题目
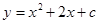 .
.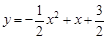 .
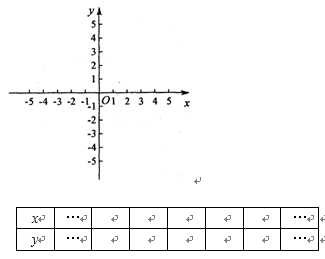
.
 y>
y>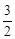 时自变量x的取值范围.
时自变量x的取值范围.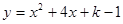 。
。 轴有两个不同的交点,求
轴有两个不同的交点,求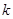 的取值范围;
的取值范围;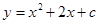 .
.