Question

【题目】因为一次函数与的图象关于轴对称，所以我们定义:函数与互为“镜子”函数.

(1)请直接写出函数的“镜子”函数：________.

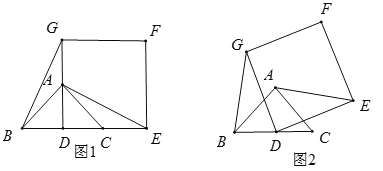
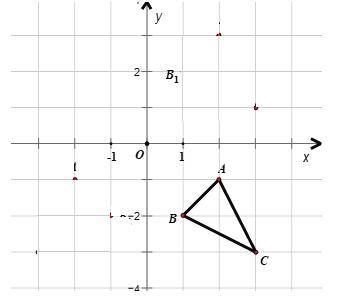
(2)如图，一对“镜子”函数与的图象交于点，分别与轴交于两点，且AO=BO，△ABC的面积为，求这对“镜子”函数的解析式.

Answer 1

【答案】(1)y=-3x-2；(2)；.

【解析】

（1）根据“镜子”函数的定义解答即可；

（2）根据“镜子”函数的定义可得与的图象关于轴对称，即可得出AO=BO=CO，设OA=OB =OC=x，根据△ABC的面积为列方程求出x的值，即可得点A、B、C的坐标，利用待定系数法求出k、b的值即可得答案.

(1)∵函数与互为“镜子”函数.

∴函数的“镜子”函数是，

故答案为：

(2)∵函数与是一对“镜子”函数，

∴一次函数与的图象关于轴对称，

∴BO=CO，

∴AO=BO=CO，

设，根据题意可得

解得

∴，

将B、A的坐标分别代入中得，

解得：

∴其函数解析式为，

∴其“镜子”函数解析式为.

∴这对“镜子”函数的解析式为和.