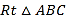Question

【题目】如图，在长方形ABCD的边CD上适当选定一点E，沿直线AE把△ADE折叠，使点D恰好落在边BC上的点F处．已知AB＝6cm，△ABF的面积是24cm2．

（1）求BF的长；

（2）求AD的长；

（3）求点E与点C的距离．

Answer 1

【答案】（1）8cm；（2）10cm；（3）cm

【解析】

（1）由在长方形ABCD中，AB＝6cm，△ABF的面积是24cm2，即可求得BF的长；

（2）由（1），易得AD＝AF，DE＝EF，即可求得AF的长，然后得出AD的长；

（3）首先设EC＝xcm，则EF＝DE＝（6﹣x）cm．由勾股定理得：CE2+CF2＝EF2求出x的值即可得出答案．

（1）∵ABCD是长方形，

∴△ABF是直角三角形，

∵△ABF面积是24cm2，

∴ABBF＝24．

∵AB＝6cm，

∴BF＝8cm；

（2）由题意知，△ADE和△AFE重合，

则△ADE≌△AFE，

则AD＝AF，DE＝EF．

在Rt△ABF中，由勾股定理得（cm）．

则AD＝10cm；

（3）∵BC＝AD＝10cm，

∴CF＝BC﹣BF＝2cm.

设EC＝xcm，则EF＝DE＝（6﹣x）cm．

由勾股定理得：CE2+CF2＝EF2，

∴x2+22＝（6﹣x）2，

解得： ，

∴点E与点C间的距离是cm.