题目内容
在实数范围内,等式 +
+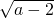 -b+3=0成立,则ab=________.
-b+3=0成立,则ab=________.
8
分析:先根据二次根式有意义的条件求出a的值,再代入解方程求出b的值,从而得到ab的值.
解答:∵2-a≥0,
∴a≤2;
∵a-2≥0,
∴a≥2;
∴a=2.
将a=2代入 +
+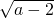 -b+3=0,可得
-b+3=0,可得
-b+3=0,
解得b=3.
∴ab=23=8.
故答案为:8.
点评:本题主要考查了二次根式的意义和性质.概念:式子 (a≥0)叫二次根式.
(a≥0)叫二次根式.
性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.
分析:先根据二次根式有意义的条件求出a的值,再代入解方程求出b的值,从而得到ab的值.
解答:∵2-a≥0,
∴a≤2;
∵a-2≥0,
∴a≥2;
∴a=2.
将a=2代入
 +
+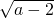 -b+3=0,可得
-b+3=0,可得-b+3=0,
解得b=3.
∴ab=23=8.
故答案为:8.
点评:本题主要考查了二次根式的意义和性质.概念:式子
 (a≥0)叫二次根式.
(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
相关题目



