题目内容
 如图,AB=3,CB=4,∠ABC=90°,CD=13,AD=12.求该图形的面积.
如图,AB=3,CB=4,∠ABC=90°,CD=13,AD=12.求该图形的面积.
 解:连接AC,
解:连接AC,∵在Rt△ACB中,AB=3,CB=4,
∴AC=
 =5,
=5,在△ACD中,
∵AC2+AD2=52+122=132=DC2,
∴△ADC为直角三角形;
∴图形面积为:
S△ADC-S△ACB=
 ×5×12-
×5×12- ×3×4=24.
×3×4=24.分析:连接AC,在Rt△ACB中,AB=3,CB=4,可求AC;在△ADC中,由勾股定理的逆定理可证△ADC为直角三角形,利用两个直角三角形的面积差求图形的面积.
点评:本题主要考查了勾股定理及其逆定理的运用,三角形面积的求法.关键是掌握勾股定理与逆定理.

练习册系列答案
相关题目
 如图,AB∥CD,CB平分∠ACD,∠A=120°,试求∠B的度数.
如图,AB∥CD,CB平分∠ACD,∠A=120°,试求∠B的度数.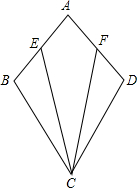 已知:如图,AB=AD,CB=CD,E、F分别是AB、AD的中点.求证:CE=CF.
已知:如图,AB=AD,CB=CD,E、F分别是AB、AD的中点.求证:CE=CF. 如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是
如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是 如图,AB=3,CB=4,∠ABC=90°,CD=13,AD=12.求该图形的面积.
如图,AB=3,CB=4,∠ABC=90°,CD=13,AD=12.求该图形的面积.