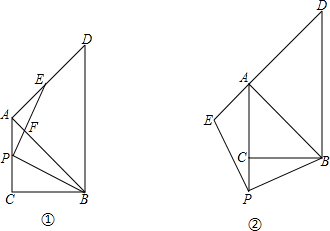
题目内容
已知△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连结BM。
(1)如图1,点D在AB上,连结DM,并延长DM交BC于点N,请探究得出BD与BM的数量关系为_______。
 |
|
(2)如图2,点D不在AB上,(1)中的结论还成立吗?如果成![]() 立,请证明;如果不成立,请说明理由。
立,请证明;如果不成立,请说明理由。

![]()

(1)![]() -------2分
-------2分
(2) 结论成立。 证明:过点C作CF∥ED,
与DM的延长线交于点F,证得△MDE≌△MFC,
∴DM=FM,DE=FC,
∴AD=ED=FC,
作AN⊥EC于点N,
由已 知∠ADE=90°,∠AB
知∠ADE=90°,∠AB![]() C=90°,
C=90°,
可证得∠1=∠2,∠3=∠4,
∵CF∥ED, ∴![]() ∠2=∠FCM,
∠2=∠FCM,
∴∠BCF=∠4+∠FCM=∠3+∠2=∠BAD,∴△BCF≌△BAD,
∴BF=BD,∠5=∠6, ∴∠DBF=∠5+∠ABF=∠6+∠ABF=∠ABC=90°,
∴△DBF是等腰直角三角形, ∵点M是DF的中点,
则△BMD是等腰直角三角形,∴BD=![]() BM.
BM. ![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE.
(2012•南岗区二模)如图,已知△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,求证:AD=CE. 如图,已知△ABC和△BAD中,AC=DB,若不增加任何字母与辅助线,要证明△ABC≌△BAD;则还需要增加一个条件是
如图,已知△ABC和△BAD中,AC=DB,若不增加任何字母与辅助线,要证明△ABC≌△BAD;则还需要增加一个条件是