��Ŀ����
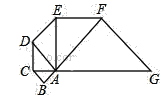
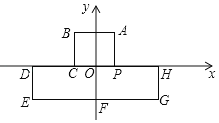
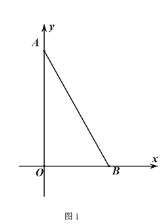
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��![]() ��������������
��������������![]()
![]() �ij�Ϊ
�ij�Ϊ![]() ������
������![]() �Dz���ʽ
�Dz���ʽ![]() �����������
�����������
��1����![]() �ij�
�ij�
��2������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() �ϴ�
�ϴ�![]() ����
����![]() ���˶�����
���˶�����![]() �ij���Ϊ
�ij���Ϊ![]() �˶�ʱ��Ϊ
�˶�ʱ��Ϊ![]() �����ú�
�����ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() ��
��
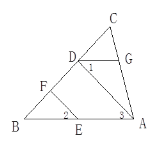
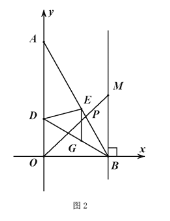
��3����ͼ2���ڣ�2�����������£�![]() ƽ��
ƽ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ�����
�ϣ�����![]() ����
����![]() ����
����![]() ���
���![]() ��������IJ�Ϊ
��������IJ�Ϊ![]() ������
������![]() �����ӳ�����
�����ӳ�����![]() ������
������![]() �ᴹֱ��ֱ����
�ᴹֱ��ֱ����![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ������
������![]() ��ֵ��
��ֵ��
���𰸡���1��10��2��d��102t��0��t��5����3��t=3��![]() =3
=3
��������
��1���Ƚⲻ��ʽ![]() �ã�a��11������ȷ����a�����ɵó����ۣ�
�ã�a��11������ȷ����a�����ɵó����ۣ�
��2�����˶�֪AP��2t�����ɵó����ۣ�
��3�����жϳ���DEN�ա�DEG��SAS�����ó���BND����DGE����EDN����EDB��45![]() ��������BDN��90
��������BDN��90![]() ������ͬ�ǣ���Ƚǣ����������жϳ���DGE����BDO���ó�EG��OD���������EG��2������S��OBP��S��BPM��3��2���ó�
������ͬ�ǣ���Ƚǣ����������жϳ���DGE����BDO���ó�EG��OD���������EG��2������S��OBP��S��BPM��3��2���ó�![]() �������ó�
�������ó�![]() ����
����![]() �����AP��6�����ɵó����ۣ�
�����AP��6�����ɵó����ۣ�
��1���ⲻ��ʽ����ʽ![]() �ã�a��11��
�ã�a��11��
��a�Dz���ʽ![]() ����������⣬
����������⣬
��a��10��
��AB�ij�Ϊa��
��AB�ij�Ϊ10��
��2���ɣ�1��֪��AB��10��
���˶�֪��AP��2t��
��d=BP��ABAP��102t��0��t��5����
��3����ͼ2����EA�Ͻ�ȡEN��EG��
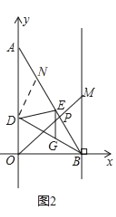
�ߡ�AED����GED��DE��DE��
���DEN�ա�DEG��SAS����
���BND����DGE����EDN����EDB��45![]() ��
��
���BDN����EDB����EDN��90![]() ��
��
���BND����DBN��90![]() ��
��
���DGE����DBN��90![]() ��
��
��BDƽ�֡�ABO��y���ڵ�D��
���DBN����DBO��
���DGE����DBO��90![]() ��
��
�ߡ�BDO����DBO��90![]() ��
��
���DGE����BDO��
��EG��OD��
�ߵ�E���G��������IJ�Ϊ2��
��EG��2��
��S��OBP��S��BPM��3��2��
��S��OBM��S��BPM��5��2��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��AP��6��
��t��6��2��3�룬![]() =
=![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�