题目内容
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,动点
,动点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .设
.设![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .设四边形
.设四边形![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() (平方单位),
(平方单位),![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.

(1)求![]() 的长;
的长;
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)求![]() 与
与![]() 的函数关系式,并直接写出自变量取值范围.
的函数关系式,并直接写出自变量取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)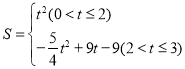 .
.
【解析】
(1)根据直线与坐标的交点求法,直线求出A,B两点的坐标.
(2)由![]() ,得出
,得出![]() ,再利用旋转的性质与等量代换,得出
,再利用旋转的性质与等量代换,得出![]() ,
,![]() ,求得四边形
,求得四边形![]() 是平行四边形.
是平行四边形.
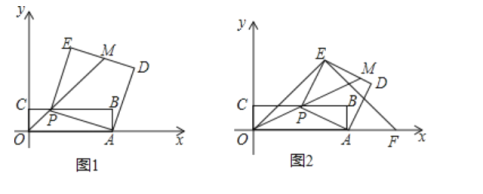
(3)要对问题分类讨论,当![]() 时,四边形在三角形ABO内部时的重叠部分面积;当
时,四边形在三角形ABO内部时的重叠部分面积;当![]() 时,四边形有部分不在三角形ABO内时重叠部分面积.
时,四边形有部分不在三角形ABO内时重叠部分面积.
(1)∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
(2)∵![]() ∴
∴![]()
由旋转知![]() ,
,![]()
∴![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
(3)∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]()
∴![]() ,
,![]() ∴
∴![]()
过点![]() 作
作![]() 于点
于点![]()
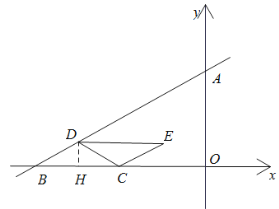
∵![]() ∴
∴![]()
∴![]()
∴当![]() 时
时![]()
当![]() 时
时
∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]()
∴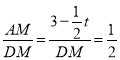 ∴
∴![]()
∴![]()
∵平行四边形![]() ∴
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴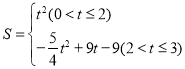
【点晴】
本题主要考查了一次函数与坐标轴的交点,平行四边形的判定,三角函数,平行四边形面积的求法以及分类的思想等知识;本题难点是对重叠部分进行分类,以及重叠部分面积的求法.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目