题目内容
20.如图(1),∠AOB=120°,在∠AOB内作两条射线OC和OD,且OM平分∠AOD,ON平分∠BOC.①若∠AOC:∠COD:∠DOB=5:3:4,求∠MON的度数.
②若将图(1)中的∠COD绕点O顺时针转一个小于70°的角α如图(2),其它条件不变,请直接写出∠MON的度数.

分析 (1)先根据∠AOC:∠COD:∠DOB=5:3:4,设∠AOC=5x,∠COD=3x,∠DOB=4x,再根据∠AOC+∠COD+∠BOD=120°,列出方程5x+3x+4x=120°,求得x的值后,得出∠AOC=50°,∠COD=30°,∠DOB=40°,再根据∠MON=∠DOM+∠CON-∠COD进行计算,即可∠MON的度数;
(2)先根据OM平分∠AOD,ON平分∠BOC,得出∠DOM=$\frac{1}{2}$∠AOD,∠CON=$\frac{1}{2}$∠BOC,再根据∠MON=∠DOM+∠CON-∠COD=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠BOC-∠COD=$\frac{1}{2}$(∠AOD+∠BOC)-∠COD=$\frac{1}{2}$(∠AOB+∠COD)-∠COD进行计算,即可得出∠MON的度数.
解答  解:(1)如图1,∵∠AOC:∠COD:∠DOB=5:3:4,
解:(1)如图1,∵∠AOC:∠COD:∠DOB=5:3:4,
∴可设∠AOC=5x,∠COD=3x,∠DOB=4x,
∵∠AOB=120°,
∴∠AOC+∠COD+∠BOD=120°,
∴5x+3x+4x=120°,
解得x=10°,
∴∠AOC=50°,∠COD=30°,∠DOB=40°,
∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=$\frac{1}{2}$∠AOD=$\frac{1}{2}$(50°+30°)=40°,
∠CON=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(30°+40°)=35°,
∴∠MON=∠DOM+∠CON-∠COD=40°+35°-30°=45°;
(2)如图2,∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=$\frac{1}{2}$∠AOD,∠CON=$\frac{1}{2}$∠BOC,
∴∠MON=∠DOM+∠CON-∠COD
=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠BOC-∠COD
=$\frac{1}{2}$(∠AOD+∠BOC)-∠COD
=$\frac{1}{2}$(∠AOB+∠COD)-∠COD
=$\frac{1}{2}$∠AOB-$\frac{1}{2}$∠COD
=$\frac{1}{2}$×120°-$\frac{1}{2}$×30°
=45°.
点评 本题主要考查了角的计算以及角平分线的定义的运用,解决问题的关键是根据角的和差关系进行计算求解,其难点在于将∠MON用∠DOM+∠CON-∠COD进行表示,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案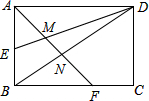 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE,DB相交于点M,N.
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE,DB相交于点M,N.(1)求$\frac{EM}{DM}$的值;
(2)求AM和MN的长.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
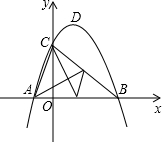 如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(A,B分别在原点的左右两侧),与y轴交于点C,抛物线的顶点为点D,且OA:OB:OC=1:3:3,求抛物线的解析式及顶点D的坐标.
如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(A,B分别在原点的左右两侧),与y轴交于点C,抛物线的顶点为点D,且OA:OB:OC=1:3:3,求抛物线的解析式及顶点D的坐标.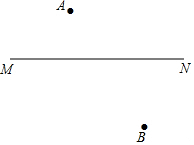 A、B为直线MN外两点,且在MN异侧,A、B到MN的距离不相等,试求一点P,满足下条件:
A、B为直线MN外两点,且在MN异侧,A、B到MN的距离不相等,试求一点P,满足下条件: