题目内容
已知x1,x2是方程x2-2x+a-1=0的两个实数根.
(1)若 ,求x1,x2及a的值;
,求x1,x2及a的值;
(2)若s=x1x2的值,求s的取值范围.
解:(1)∵x1,x2是方程x2-2x+a-1=0的两个实数根,
∴x1+x2=2 ①
∵ ②
②
∴①与②组成方程组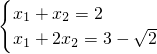 ,
,
解得:x1=1+ x2=1-
x2=1- ,
,
∵x1•x2=a-1=(1+ )•(1-
)•(1- )=-1
)=-1
解得:a=0;
(2)∵x1,x2是方程x2-2x+a-1=0的两个实数根,
∴(-2)2-4(a-1)>0
解得:a<2
∴s=x1x2=a-1
∴s<1.
分析:(1)根据两根之和和 组成二元一次方程组求解即可;
组成二元一次方程组求解即可;
(2)利用根的判别式得到a的取值范围,进而可以求得s的取值范围.
点评:本题考查了根与系数的关系,解题的关键是根据根与系数得到有关a的方程或不等式.
∴x1+x2=2 ①
∵
 ②
②∴①与②组成方程组
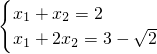 ,
,解得:x1=1+
 x2=1-
x2=1- ,
,∵x1•x2=a-1=(1+
 )•(1-
)•(1- )=-1
)=-1解得:a=0;
(2)∵x1,x2是方程x2-2x+a-1=0的两个实数根,
∴(-2)2-4(a-1)>0
解得:a<2
∴s=x1x2=a-1
∴s<1.
分析:(1)根据两根之和和
 组成二元一次方程组求解即可;
组成二元一次方程组求解即可;(2)利用根的判别式得到a的取值范围,进而可以求得s的取值范围.
点评:本题考查了根与系数的关系,解题的关键是根据根与系数得到有关a的方程或不等式.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知x1,x2是方程x2+3x+1=0的两个实数根,则x13+8x2+20=( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|