题目内容
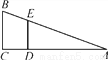
如图,某班上体育课,甲、乙两名同学分别站在点C,D的位置时,乙的影子恰好在甲的影子里边,已知甲身高1.8米,乙身高1.5米,甲的影长是6米,则甲、乙同学相距____米.
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
题目内容
如图,某班上体育课,甲、乙两名同学分别站在点C,D的位置时,乙的影子恰好在甲的影子里边,已知甲身高1.8米,乙身高1.5米,甲的影长是6米,则甲、乙同学相距____米.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案