题目内容
⊙O的内接正三角形的边心距为4cm，则⊙O的面积为________，该正三角形的边长为________．
64πcm2 8
cm
分析：根据正三角形的性质得出：∠ACO=∠OCB=30°，进而得出CO以及CD的长即可．
解答：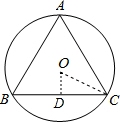
解：过点O作OD⊥BC于点D，
∵⊙O的内接正三角形的边心距为4cm，
∴OD=4cm，
由正三角形的性质可得出：∠ACO=∠OCB=30°，
∴CO=2DO=8cm，
∴⊙O的面积为：π×82=64π（cm2），
∴CD=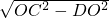
=8（cm），
故答案为：64πcm2，8cm．
点评：此题主要考查了正多边形和圆的性质，根据已知得出∠ACO=∠OCB=30°是解题关键．
cm分析：根据正三角形的性质得出：∠ACO=∠OCB=30°，进而得出CO以及CD的长即可．
解答：
解：过点O作OD⊥BC于点D，∵⊙O的内接正三角形的边心距为4cm，
∴OD=4cm，
由正三角形的性质可得出：∠ACO=∠OCB=30°，
∴CO=2DO=8cm，
∴⊙O的面积为：π×82=64π（cm2），
∴CD=
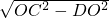=8（cm），故答案为：64πcm2，8
cm．点评：此题主要考查了正多边形和圆的性质，根据已知得出∠ACO=∠OCB=30°是解题关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
圆的内接正三角形的半径与边心距的比为（ ）
| A、1：2 | ||
| B、2：1 | ||
C、
| ||
D、2：
|
已知二次函数y=x2-2mx+4m-8