题目内容
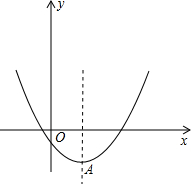 已知二次函数y=x2-2mx+4m-8
已知二次函数y=x2-2mx+4m-8(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2-2mx+4m-8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2-2mx+4m-8与x轴交点的横坐标均为整数,求整数m的最小值.
分析:(1)求出二次函数的对称轴x=m,由于抛物线的开口向上,在对称轴的左边y随x的增大而减小,可以求出m的取值范围.
(2)在抛物线内作出正三角形,求出正三角形的边长,然后计算三角形的面积,得到△AMN的面积是m无关的定值.
(3)当y=0时,求出抛物线与x轴的两个交点的坐标,然后确定整数m的值.
(2)在抛物线内作出正三角形,求出正三角形的边长,然后计算三角形的面积,得到△AMN的面积是m无关的定值.
(3)当y=0时,求出抛物线与x轴的两个交点的坐标,然后确定整数m的值.
解答:解:(1)二次函数y=x2-2mx+4m-8的对称轴是:x=m.
∵当x≤2时,函数值y随x的增大而减小,
而x≤2应在对称轴的左边,
∴m≥2.
(2)如图:顶点A的坐标为(m,-m2+4m-8)
△AMN是抛物线的内接正三角形,
MN交对称轴于点B,tan∠AMB=tan60°=
=
,
则AB=
BM=
BN,
设BM=BN=a,则AB=
a,
∴点M的坐标为(m+a,
a-m2+4m-8),
∵点M在抛物线上,
∴
a-m2+4m-8=(m+a)2-2m(m+a)+4m-8,
整理得:a2-
a=0
得:a=
(a=0舍去)
所以△AMN是边长为2
的正三角形,
S△AMN=
×2
×3=3
,与m无关;
(3)当y=0时,x2-2mx+4m-8=0,
解得:x=m±
=m±
,
∵抛物线y=x2-2mx+4m-8与x轴交点的横坐标均为整数,
∴(m-2)2+4应是完全平方数,
∴m的最小值为:m=2.
∵当x≤2时,函数值y随x的增大而减小,
而x≤2应在对称轴的左边,
∴m≥2.
(2)如图:顶点A的坐标为(m,-m2+4m-8)
△AMN是抛物线的内接正三角形,
MN交对称轴于点B,tan∠AMB=tan60°=
| AB |
| BM |
| 3 |
则AB=
| 3 |
| 3 |
设BM=BN=a,则AB=
| 3 |

∴点M的坐标为(m+a,
| 3 |
∵点M在抛物线上,
∴
| 3 |
整理得:a2-
| 3 |
得:a=
| 3 |
所以△AMN是边长为2
| 3 |
S△AMN=
| 1 |
| 2 |
| 3 |
| 3 |
(3)当y=0时,x2-2mx+4m-8=0,
解得:x=m±
| m2-4m+8 |
| (m-2)2+4 |
∵抛物线y=x2-2mx+4m-8与x轴交点的横坐标均为整数,
∴(m-2)2+4应是完全平方数,
∴m的最小值为:m=2.
点评:本题考查的是二次函数的综合题,(1)利用二次函数的对称轴确定m的取值范围.(2)由点M在抛物线上,求出正三角形的边长,计算正三角形的面积.(3)根据抛物线与x轴的交点的横坐标都是整数,确定整数m的值.

练习册系列答案
相关题目
已知二次函数y=x2+(2a+1)x+a2-1的最小值为0,则a的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).