题目内容
已知∠BOD=2∠AOB,OC平分∠AOD,∠BOC=20°,则∠AOB度数是 .
考点:角平分线的定义
专题:
分析:根据角平分线的性质,可得∠AOC=∠DOC=
∠AOD,根据角的和差,可得
| 1 |
| 2 |
解答:解:由∠BOD=2∠AOB,得∠AOB=∠AOD.
由OC平分∠AOD,得∠AOC=
∠AOD=
∠AOB.
由角的和差,得∠BOC=∠AOB+∠AOC=∠AOB+
∠AOB=20°.
∠AOB=(
)°,
故答案为:(
)°.
由OC平分∠AOD,得∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠BOC=∠AOB+∠AOC=∠AOB+
| 1 |
| 2 |
∠AOB=(
| 40 |
| 3 |
故答案为:(
| 40 |
| 3 |
点评:本题考查了角平分线的定义,利用了角平分线的性质,角的和差.

练习册系列答案
相关题目
若x1,x2是一元二次方程2x2+5x-6=0的两个根,则x1+x2和x1•x2的值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
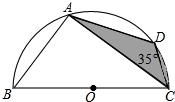 如图,半圆直径BC=10,AB=AD,∠ACD=35°,求阴影部分面积.
如图,半圆直径BC=10,AB=AD,∠ACD=35°,求阴影部分面积. 如图是中央电视台“大风车”栏目标志的一部分,由图形旋转的知识可知,这个图形可以看作是一个“半圆”图形绕着
如图是中央电视台“大风车”栏目标志的一部分,由图形旋转的知识可知,这个图形可以看作是一个“半圆”图形绕着 如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=8,则DG+EH+FI的长是多少?
如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=8,则DG+EH+FI的长是多少? 如图,已知AC∥DE,∠1=∠2,求证:∠B=∠DCE.
如图,已知AC∥DE,∠1=∠2,求证:∠B=∠DCE. 如图,阴影部分占大正方形的
如图,阴影部分占大正方形的