题目内容
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③2a+b>0;④9a+3b+c<0;⑤8a+c>0.其中,结论正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③2a+b>0;④9a+3b+c<0;⑤8a+c>0.其中,结论正确的是考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
解答:解:①∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,
∴b2-4ac>0,
故本选项正确;
②∵该抛物线的开口方向向上,
∴a>0;
∵该抛物线与y轴交于负半轴,
∴c<0,
根据图象知,对称轴x=-
=1,
∴b=-2a<0,即b<0;
∴abc>0
故本选项正确;
③根据图象知,对称轴x=-
=1,
∴b=-2a;
∴2a+b=0;
故本选项错误;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;
故本选项正确;
⑤∵对称轴x=-
=1,
∴b=-2a,
可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,
故本选项正确;
综上所述,正确的说法是:①②④⑤.
故答案是:①②④⑤.
∴b2-4ac>0,
故本选项正确;
②∵该抛物线的开口方向向上,
∴a>0;
∵该抛物线与y轴交于负半轴,
∴c<0,
根据图象知,对称轴x=-
| b |
| 2a |
∴b=-2a<0,即b<0;
∴abc>0
故本选项正确;
③根据图象知,对称轴x=-
| b |
| 2a |
∴b=-2a;
∴2a+b=0;
故本选项错误;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;
故本选项正确;
⑤∵对称轴x=-
| b |
| 2a |
∴b=-2a,
可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,
故本选项正确;
综上所述,正确的说法是:①②④⑤.
故答案是:①②④⑤.
点评:主要考查图象与二次函数系数之间的关系,解题的关键是会利用对称轴的范围求a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
 如图,已知点C在点B的北偏西65°方向,点B在点A的北偏东35°方向,则∠ABC的度数为( )
如图,已知点C在点B的北偏西65°方向,点B在点A的北偏东35°方向,则∠ABC的度数为( )| A、65° | B、35° |
| C、80° | D、70° |
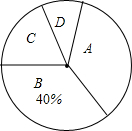 为了了解我校九年级男生立定跳远的成绩,从全校随机抽50名男生的测试成绩进行调查.根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成统计表和扇形图,如图:
为了了解我校九年级男生立定跳远的成绩,从全校随机抽50名男生的测试成绩进行调查.根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成统计表和扇形图,如图: 已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数y=
已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数y=