题目内容
9. 如图,△ABC中,∠C=90°,AB=13,AC=5,BC=12,点O为∠CAB和∠CBA的平分线的交点,则OP=2.
如图,△ABC中,∠C=90°,AB=13,AC=5,BC=12,点O为∠CAB和∠CBA的平分线的交点,则OP=2.
分析 作OE⊥BC,OF⊥AC,根据垂直定义得出∠C=∠CFO=∠OEC=90°,即可推出四边形CFOE是矩形,根据角平分线性质求出OE=OF=OP,即可推出矩形CFOE是正方形,设OE=OP=OF=x,则AP=AF=5-x,BP=BE=12-x,根据PA+PB=AB=13,列出等式即可解得.
解答  解:作OE⊥BC,OF⊥AC,
解:作OE⊥BC,OF⊥AC,
∴∠C=∠CFO=∠OEC=90°,
∴四边形CFOE是矩形;
∵∠CAB,∠CBA的平分线相交于点O,OE⊥BC,OF⊥AC,OP⊥AB,
∴OE=OP=OF,
∴四边形CFOE是正方形,
设OE=OP=OF=x,则AP=AF=5-x,BP=BE=12-x,
∴5-x+12-x=13,
解得x=2,
∴OP=OE=2.
故答案为2.
点评 本题考查了角平分线的性质,正方形的判定,证得四边形CFOE是正方形是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
18.若关于x的分式方程$\frac{m}{x-5}$=$\frac{x-1}{x-5}$无解,则m的值为( )
| A. | -4 | B. | 4 | C. | -6 | D. | 6 |
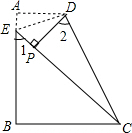 下图是一张四边形ABCD纸片,∠A=90°,AD∥BC,沿虚线DE折叠,使点A落在四边形DEBC的内部点P处.
下图是一张四边形ABCD纸片,∠A=90°,AD∥BC,沿虚线DE折叠,使点A落在四边形DEBC的内部点P处.