题目内容
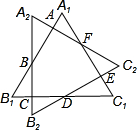 如图:边长为1的正△A1B1C1的中心为O,将正△A1B1C1绕中心O旋转到△A2B2C2,使得A2B2⊥B1C1.则两三角形的公共部分(即六边形ABCDEF)的面积为________.
如图:边长为1的正△A1B1C1的中心为O,将正△A1B1C1绕中心O旋转到△A2B2C2,使得A2B2⊥B1C1.则两三角形的公共部分(即六边形ABCDEF)的面积为________.
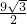 -
-
分析:连接OB1、OC1、OA2、OB2,根据O为等边三角形的中心,得出∠A2OB2=∠B1OC1=120°,求出∠A2ON=∠C1OM,根据ASA证△A2ON≌△C1OM,推出ON=OM,推出B1N=B2M,设B1N=B2M=x,根据∠OB1B=∠OB1C=30°=∠B1BN,求出BN=x,推出CN=
 x,B1C=
x,B1C= x,BB1=2B1C=
x,BB1=2B1C= x,同理CD=BC=x+
x,同理CD=BC=x+ x=
x= x,C1D=BB1=
x,C1D=BB1= x,依题意列方程B1C+CD+DC1=1,求x的值,根据S六边形ABCDEF=S△A2B2C2-3S△B2CD求解.
x,依题意列方程B1C+CD+DC1=1,求x的值,根据S六边形ABCDEF=S△A2B2C2-3S△B2CD求解.解答:
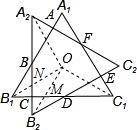
连接OB1、OC1、OA2、OB2,
∵O为等边三角形的中心,
∴∠A2OB2=∠B1OC1,
∴都减去∠B1OB2得:∠A2ON=∠C1OM,
在△A2ON和△C1OM中
∵
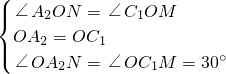 ,
,∴△A2ON≌△C1OM,
∴ON=OM,
∵OB2=OB1,
∴B1N=B2M,
设B1N=B2M=x,
∵∠OB1B=∠OB1C=30°=∠B1BN,
∴BN=x,
∴CN=
 x,B1C=
x,B1C= x,BB1=2B1C=
x,BB1=2B1C= x,
x,同理CD=BC=x+
 x=
x= x,C1D=BB1=
x,C1D=BB1= x
x依题意B1C1=B1C+CD+DC1=1,
 x+
x+ x+
x+ x=1,
x=1,x=
 -1,
-1,∴B2C=
 ×(
×( -1)=
-1)= -
- ,CD=
,CD= ×(
×( -1)=
-1)= -
-
∴S六边形ABCDEF=S△A2B2C2-3S△B2CD
=
 ×1×
×1× -3×
-3× ×(
×( -
- )×(
)×( -
- ),
),=
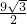 -
-
故答案为:
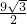 -
- .
.点评:本题考查了旋转的性质,等边三角形的性质.关键是根据条件,得出特殊三角形,全等三角形,利用“割补法”求面积.

练习册系列答案
相关题目
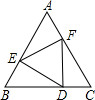 如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )
如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
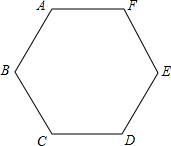 已知:如图,边长为a的正六边形ABCDEF.
已知:如图,边长为a的正六边形ABCDEF.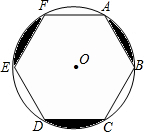 如图,边长为2的正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为
如图,边长为2的正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为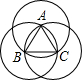 如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为
如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为 如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )
如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )