Question

【题目】如图，点M是线段AB中点，AD、BC交于点N，连接AC、BD、MC、MD，∠l=∠2，∠3=∠4．

（1）求证：△AMD≌△BMC；

（2）图中在不添加新的字母的情况下，请写出除了“△AMD≌△BMC”以外的所有全等三角形，并选出其中一对进行证明．

Answer 1

【答案】（1）详见解析；（2）△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．

【解析】

（1）根据ASA即可判断；（2）全等三角形有：△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．根据三角形全等的判定方法一一判断即可.

（1）∵点M是AB中点，

∴AM=BM，

∵∠1=∠2，

∴∠AMD=∠BMC，

在△AMD和△BMC中，

，

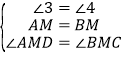∴△AMD≌△MBC（ASA）；

（2）△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．

理由：∵△AMD≌△MBC，

∴AD=BC，

∵∠3=∠4，AB=BA，

∴△BAD≌△ABC（SAS），

∴AC=BD，∠BDN=∠ACN，

∵∠ANC=∠BND，

∴△ANC≌△BND（AAS），

∵AC=BD，∠CAM=∠DBM，AM=BM，

∴△AMC≌△BMD（SAS）．