题目内容
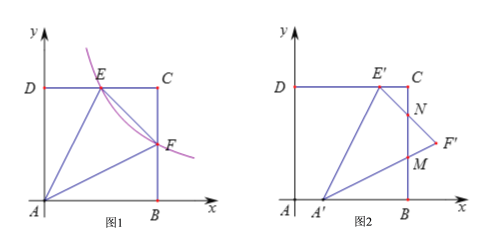
【题目】如图1,正方形ABCD的边长为4,以AB所在的直线为x轴,以AD所在的直线为y轴建立平面直角坐标系![]() 反比例函数
反比例函数![]() 的图象与CD交于E点,与CB交于F点.
的图象与CD交于E点,与CB交于F点.
(1)求证:![]() ;
;
(2)若![]() 的面积为6,求反比例函数的解析式;
的面积为6,求反比例函数的解析式;
(3)在(2)的条件下,将![]() 沿x轴的正方向平移1个单位后得到
沿x轴的正方向平移1个单位后得到![]() ,如图2,线段
,如图2,线段![]() 与
与![]() 相交于点M,线段
相交于点M,线段![]() 与BC相交于点N.求
与BC相交于点N.求![]() 与正方形ABCD的重叠部分面积.
与正方形ABCD的重叠部分面积.
【答案】(1)证明见解析;(2)反比例函数解析式为![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】(1)根据反比例函数图象上点的坐标特点可得出DE=BF,故可得出结论;
(2)设DE=BF=a,则CE=4-a,CF=4-a,再由S△AEF=S正方形ABCD-S△ADE-S△ABF-S△ECF即可得出a的值,进而可得出反比例函数的解析式;
(3)根据题意求得N点的坐标,再求出直线![]() 的解析式,进而得到M点的坐标,然后由阴影部分分解图形的面积公式求解即可.
的解析式,进而得到M点的坐标,然后由阴影部分分解图形的面积公式求解即可.
(1)由题意知:![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中
中
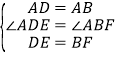
∴![]() ≌
≌![]() (SAS)
(SAS)
∴![]() .
.
(2)由(1)知:![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴反比例函数解析式为:![]() .
.
(3)由题意得:![]() ,
,![]() ,
,![]()
由(1)知:![]()
∴![]()
设直线![]() 的解析式为:
的解析式为:![]()
把点![]() ,
,![]() 代入得:
代入得:
![]()
解之得: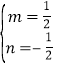
∴![]()
∴![]()
∴![]()
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目