题目内容
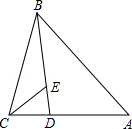
已知等腰三角形ABC中,∠ACB=90°,点E在AC边的延长线上,且∠DEC=45°,点M、N分别是DE、AE的中点,连接MN交直线BE于点F.当点D在CB边上时,如图1所示,易证MF+FN= BE
BE
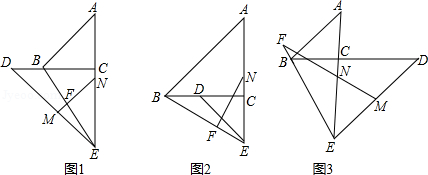
(1)当点D在CB边上时,如图2所示,上述结论是否成立?若成立,请给与证明;若不成立,请写出你的猜想,并说明理由.
(2)当点D在BC边的延长线上时,如图3所示,请直接写出你的结论.(不需要证明)
 BE
BE
(1)当点D在CB边上时,如图2所示,上述结论是否成立?若成立,请给与证明;若不成立,请写出你的猜想,并说明理由.
(2)当点D在BC边的延长线上时,如图3所示,请直接写出你的结论.(不需要证明)
(1)不成立。猜想:FN﹣MF= BE。理由见解析
BE。理由见解析
(2)MF﹣FN= BE。
BE。
 BE。理由见解析
BE。理由见解析(2)MF﹣FN=
 BE。
BE。试题分析:(1)对结论作出否定,猜想FN﹣MF=
 BE,连接AD,根据M、N分别是DE、AE的中点,可得MN=
BE,连接AD,根据M、N分别是DE、AE的中点,可得MN= AD,再根据题干条件证明△ACD≌△BCE,得出AD=BE,结合MN=FN﹣MF,于是证明出猜想。
AD,再根据题干条件证明△ACD≌△BCE,得出AD=BE,结合MN=FN﹣MF,于是证明出猜想。(1)不成立。猜想:FN﹣MF=
 BE。理由如下:
BE。理由如下:如图,连接AD,.
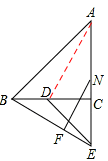
∵M、N分别是DE、AE的中点,∴MN=
 AD。
AD。∵在△ACD与△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS)。∴AD=BE。
∵MN=FN﹣MF,∴FN﹣MF=
 BE。
BE。(2)结论:MF﹣FN=
 BE,证明如下:
BE,证明如下:连接AD,
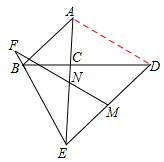
∵M、N分别是DE、AE的中点,∴MN=
 AD。
AD。∵在△ACD与△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS)。∴AD=BE。∴MN=
 BE。
BE。∵MN=FM﹣FN,∴MF﹣FN=
 BE。
BE。
练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 ,则这个多边形是【 】
,则这个多边形是【 】
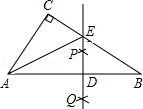
 AB的长为半径做弧,两弧相交于点P和Q.
AB的长为半径做弧,两弧相交于点P和Q.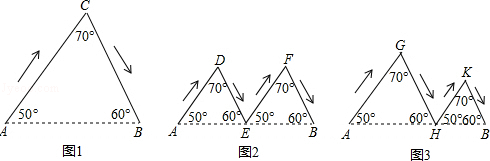

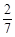 ,求这个正多边形的边数和它一个内角的度数。
,求这个正多边形的边数和它一个内角的度数。