题目内容
如图，∠A=∠C=∠BED=90°，求证：∠1=∠3，∠2=∠4．考点：直角三角形的性质
专题：证明题
分析：根据平角等于180°求出∠1+∠2=90°，再根据直角三角形两锐角互余可得∠2+∠3=90°，然后根据同角的余角相等证明即可，同理可得∠2=∠4．
解答：证明：∵∠BED=90°，
∴∠1+∠2=180°-90°=90°，
∵∠A=90°，
∴∠2+∠3=90°，
∴∠1=∠3；
同理可得∠2=∠4．
∴∠1+∠2=180°-90°=90°，
∵∠A=90°，
∴∠2+∠3=90°，
∴∠1=∠3；
同理可得∠2=∠4．
点评：本题考查了直角三角形两锐角互余的性质，同角的余角相等的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
（1）如图所示的几何图形叫做
如图，用如图的材料拼成一个圆柱，求圆柱的表面积．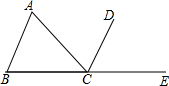
如图所示，在△ABC中，以C为顶点，在△ABC外作∠ACD=∠A，且点A和点D在直线BC的同侧，延长BC至E，在所作的图形中：若等腰三角形的两条边的长分别为3cm和7cm，则它的周长是（ ）
| A、10cm |
| B、13cm |
| C、17cm |
| D、13cm或17cm |
如图，已知点A（-1，0），B（0，2），把线段AB平移，使点B移动到点C（4，4）处，这时点A移动到点D处．