Question

圆O的半径r=

2

，弦BC=2，弦AB=

6

，则∠ABC的度数是

 

．

Answer 1

分析：此题分为两种情况：弦AB和弦BC在圆心的同侧或弦AB和弦BC在圆心的两侧．构造半径、半弦、弦心距组成的直角三角形，利用解直角三角形的知识进行解决．

解答：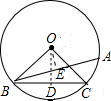
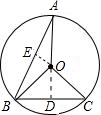
解：作OD⊥BC于D，作OE⊥AB于E．
根据垂径定理，得
BD=

1

2

BC=1；BE=

1

2

AB=

6

2

．
在直角三角形OBD中，cos∠OBD=

BD

OB

=

2

2

，
则∠OBD=45°．
在直角三角形OBE中，cos∠OBE=

BE

OB

=

3

2

，
则∠OBE=30°．
当BC和AB在圆心的同侧时，则∠ABC=∠OBC-∠OBE=15°；
当BC和AB在圆心的两侧时，则∠ABC=∠OBC+∠OBE=75°

点评：此题要特别注意两种情况：两条弦在圆心的同侧或两侧．综合运用了垂径定理和解直角三角形的知识．