题目内容
如图,一艘潜艇在海面下500米深处的A点,测得正前方俯角为31.0°方向上
的海底有黑匣子发出的信号,潜艇在同一深度保持直线航行500米,在B点处测得海底黑
 匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9° ≈ 0.60,cos36.9° ≈ 0.80,tan36.9° ≈0.75,sin31.0°≈ 0.51,cos31.0°≈0.87 ,tan31.0°≈ 0.60)
匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9° ≈ 0.60,cos36.9° ≈ 0.80,tan36.9° ≈0.75,sin31.0°≈ 0.51,cos31.0°≈0.87 ,tan31.0°≈ 0.60)
解:作CD⊥AB,垂足为D,CD交海面于H.设CD 米.
米.
在Rt△ACD中,由tan∠CAD= ,得AD=
,得AD= ,
,
 在Rt△BCD中,由tan∠CBD=
在Rt△BCD中,由tan∠CBD= ,得BD=
,得BD= .…
.…
∵AD-BD=AB,
∴ =500.
=500.
将tan31.0°≈ 0.60 ,tan36.9° ≈0. 75代入得:
解得x =1500.
∴CH=CD+DH=1500+500=2000.
答:海底黑匣子C所在点距离海面的深度约2000米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
小贝家买了一辆小轿车,小贝记录了连续七天中每天行驶的路程:
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 路程 (千米) | 43 | 29 | 27 | 52 | 43 | 72 | 33 |
则小贝家轿车这七天行驶路程的众数和中位数分别是
A.33, 52 B.43,52 C.43,43 D.52,43





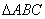 是等腰直角三角形,
是等腰直角三角形, ,点
,点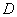 是
是 的中点.作正方形
的中点.作正方形 ,使点
,使点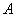 、
、 分别在
分别在 和
和 上,连接
上,连接  ,
, .
. ,
, ,当
,当 的值.
的值.
 ,求代数式
,求代数式 的值.
的值.