题目内容
如图1,已知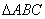 是等腰直角三角形,
是等腰直角三角形, ,点
,点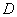 是
是 的中点.作正方形
的中点.作正方形 ,使点
,使点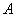 、
、 分别在
分别在 和
和 上,连接
上,连接  ,
, .
.
(1)试猜想线段 和
和 的数量关系是 ;
的数量关系是 ;
(2)将正方形 绕点
绕点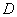 逆时针方向旋转
逆时针方向旋转 ,
,
①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;
②若 ,当
,当 取最大值时,求
取最大值时,求 的值.
的值.

解:(1) ;
;
(2)①成立.以下给出证明:
如图,连接 ,
,
∵在 Rt 中,
中,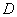 为斜边
为斜边 中点,
中点,
∴  ,
, ,
,
∴ .
.
∵四边形 为正方形,
为正方形,
∴ ,且
,且 ,
,
 ∴
∴ ,
,
∴ .
.
在 和
和 中,
中,

∴ ≌
≌ ,
,
∴ .
.
②由①可得 ,当
,当 取得最大值时,
取得最大值时, 取得最大值.
取得最大值.
当旋转角为 时,
时, ,最大值为
,最大值为 .
.
如图,此时 .
.


练习册系列答案
相关题目
 时,分式
时,分式 的值为0.
的值为0. 匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9° ≈ 0.60,cos36.9° ≈ 0.80,tan36.9° ≈0.75,sin31.0°≈ 0.51,cos31.0°≈0.87 ,tan31.0°≈ 0.60)
匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9° ≈ 0.60,cos36.9° ≈ 0.80,tan36.9° ≈0.75,sin31.0°≈ 0.51,cos31.0°≈0.87 ,tan31.0°≈ 0.60) 的坐标为(1,0),将线段
的坐标为(1,0),将线段 绕点
绕点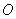 按顺时针方向旋转
按顺时针方向旋转 ,再将其长度伸长为
,再将其长度伸长为 ;又将线段
;又将线段 ,…,这样依次得到线段
,…,这样依次得到线段 ,
, ,…,
,…, .
. 的坐标为 ; 当
的坐标为 ; 当 (
( 为自然数)时,点
为自然数)时,点 的坐标为 .
的坐标为 .
 中,
中, ,
, ,
, ,连接
,连接 ,
, 的平分线交
的平分线交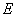 ,且
,且 .
. ,求四边形
,求四边形
 B.
B.  C.
C.  D.
D. 
 中,
中, ,
, 于点
于点 ,且
,且 ,连接
,连接 ,则
,则 的度
的度
 ,那么这个正多边形的边数是( )
,那么这个正多边形的边数是( )