题目内容
已知:点A(-1,0),点B(3,0),点C在y轴上,且三角形ABC的面积为6,则点C坐标为 .
考点:坐标与图形性质,三角形的面积
专题:分类讨论
分析:根据点A、B的纵坐标都是0判断出点A、B在x轴上,然后求出AB的长,设点C到x轴的距离为h,利用三角形的面积列式求出h,然后分两种情况讨论求解即可.
解答:解:∵点A(-1,0),点B(3,0),
∴点A、B在x轴上,AB=3-(-1)=3+1=4,
设点C到x轴的距离为h,
则
×4h=6,
解得h=3,
所以,点C的坐标为(0,3)或(0,-3).
故答案为:(0,3)或(0,-3).
∴点A、B在x轴上,AB=3-(-1)=3+1=4,
设点C到x轴的距离为h,
则
| 1 |
| 2 |
解得h=3,
所以,点C的坐标为(0,3)或(0,-3).
故答案为:(0,3)或(0,-3).
点评:本题考查了坐标与图形性质,三角形的面积,判断出A、B都在x轴上是解题的关键,易错点在于要分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、相等的角是对顶角 |
| B、一个角的余角一定是锐角 |
| C、一个角的补角一定是钝角 |
| D、同旁内角互补 |
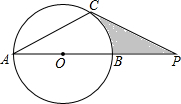 如图,⊙O的直径AB与弦AC的夹角∠A=30°,过点C作⊙O的切线交AB的延长线于点P,PC=
如图,⊙O的直径AB与弦AC的夹角∠A=30°,过点C作⊙O的切线交AB的延长线于点P,PC= 如图,△ABC中,点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4,则面积是1的三角形有
如图,△ABC中,点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4,则面积是1的三角形有