题目内容
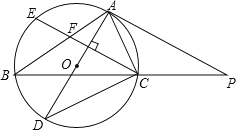
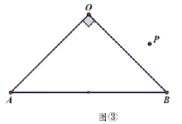
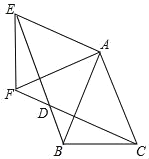
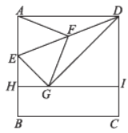
【题目】如图，正方
的边长为
，点
是边
上一点，
是
的中点，过点作
，且
，连接
，
，过
点作
，分别交，
于点
，
．
（1）求证：
；
（2）求证：
；
（3）若
，求
的长．
【答案】（1）详见解析；（2）详见解析；（3）
【解析】
（1）根据直角三角形斜边上中线的性质可得出AF=EF=DF=FG，从而得出点D，E，G三点在以DE为直径的圆上，从而得出∠EGD=90°，即可得出结论；
（2）根据正方形的性质以及余角的性质得出
，
，从而可得出结论；
（3）由（1）知点
，
，
，
在以
为直径的圆上，可得出
，进一步得出∠GDI=45°，由DG=AD=2，可求出DI，GI的长，再由（2）中的相似三角形可求得HE的长，最后可得出结果．
（1）证明：
四边形
是正方形，
，
又点
为中点，
，
，
，
点，，在以为直径的圆上，
，即
；
（2）证明：四边形是正方形，
，
，
，
由（1）知
，
，
，
；
（3）解：
，
；
由（1）知点，，，在以为直径的圆上，
，
，
，
在
中，
，
，
四边形是正方形，，
，
，
，
由（2）知
，
，
．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
