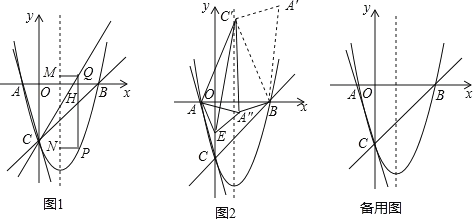
题目内容
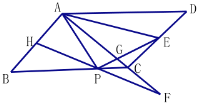
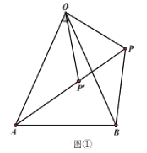
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 外一点,将
外一点,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,且点
,且点![]() 、
、![]() 、
、![]() 三点在同一直线上.
三点在同一直线上.
(1)(观察猜想)
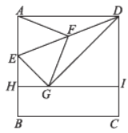
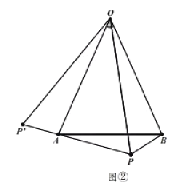
在图①中,![]() ;在图②中,
;在图②中,![]() (用含
(用含![]() 的代数式表示)
的代数式表示)
(2)(类比探究)
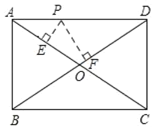
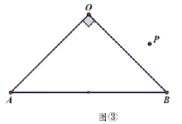
如图③,若![]() ,请补全图形,再过点
,请补全图形,再过点![]() 作
作![]() 于点
于点![]() ,探究线段
,探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)(问题解决)
若![]() ,
,![]() ,
,![]() ,求点
,求点![]() 到
到![]() 的距离.
的距离.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ,证明见解析;(3)点
,证明见解析;(3)点![]() 到
到![]() 的距离为
的距离为![]() 或
或![]() .
.
【解析】
(1)在图①中由旋转可知![]() ,由三角形内角和可知∠OAB+∠OBA+∠AOB=180°,∠PAB+∠PBA+∠APB=180°,因为
,由三角形内角和可知∠OAB+∠OBA+∠AOB=180°,∠PAB+∠PBA+∠APB=180°,因为![]() ,∠OAP+∠PAB=∠OAB,所以∠APB=∠AOB=α;在图②中,由旋转可知
,∠OAP+∠PAB=∠OAB,所以∠APB=∠AOB=α;在图②中,由旋转可知![]() ,得到∠OBP+OAP=180°,通过四边形OAPB的内角和为360°,可以得到∠AOB+∠APB=180°,因此∠APB=
,得到∠OBP+OAP=180°,通过四边形OAPB的内角和为360°,可以得到∠AOB+∠APB=180°,因此∠APB=![]() ;
;
(2)由旋转可知![]() ≌
≌![]() ,
,![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,得到
,得到![]() ,即可得证
,即可得证![]() ;
;
(3)当点![]() 在
在![]() 上方时,过点
上方时,过点![]() 作
作![]() 于点
于点![]() ,由条件可求得PA,再由
,由条件可求得PA,再由![]() 可求出OH;当点
可求出OH;当点![]() 在
在![]() 下方时,过点
下方时,过点![]() 作
作![]() 于点
于点![]() ,同理可求出OH.
,同理可求出OH.
(1)①由三角形内角和为180°得到∠OAB+∠OBA+∠AOB=180°,∠PAB+∠PBA+∠APB=180°,
由旋转可知![]() ,
,
又∵∠OAP+∠PAB=∠OAB,
∴∠OBP+∠PAB+∠ABO+∠AOB=180°,即∠PAB+∠ABP+∠AOB=180°,
∴∠APB=∠AOB=α;
②由旋转可知![]() ,
,
∵![]() =180°,
=180°,
∴∠OBP+OAP=180°,
又∵∠OBP+OAP+∠AOB+∠APB=360°,
∴∠AOB+∠APB=180°,
∴∠APB=![]() ;
;
(2)![]()
证明:由![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]()
∴![]() ≌
≌![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]()
∴![]()
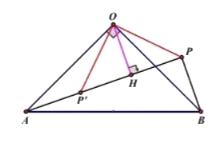
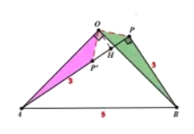
(3)【解法1】
(i)如图,当点![]() 在
在![]() 上方时,过点
上方时,过点![]() 作
作![]() 于点
于点![]()
由(1)知,![]() ,
,
∵![]()
∴![]()
由(2)知, ![]()
∴![]()
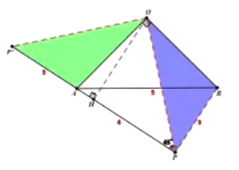
(ii)如图,当点![]() 在
在![]() 下方时,过点
下方时,过点![]() 作
作![]() 于点
于点![]()
由(1)知, ![]() ,
,
∵![]()
∴![]()
∴![]()
∴点![]() 到
到![]() 的距离为
的距离为![]() 或
或![]() .
.
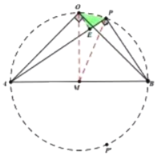
 【解法2】
【解法2】
(i)如图,当点![]() 在
在![]() 上方时 ,过点
上方时 ,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,取
,取![]() 的中点
的中点![]()
∴![]()
∴点![]() ,
,![]() ,
,![]() ,
,![]() 四点在圆
四点在圆![]() 上
上
∴![]() ,且
,且![]()
∴![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
在![]() 中,
中,![]() ,设
,设![]() ,则
,则![]()
∴![]() ,化简得:
,化简得:![]()
∴![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
∴![]()
(ii)若点![]() 在
在![]() 的下方,过点
的下方,过点![]() 作
作![]() ,
,
同理可得:![]()
∴点![]() 到
到![]() 的距离为
的距离为![]() 或
或![]() .
.

 特高级教师点拨系列答案
特高级教师点拨系列答案