题目内容
 如图,已知点O是正三角形ABC三条高的交点,现将△AOB绕点O至少要旋转
如图,已知点O是正三角形ABC三条高的交点,现将△AOB绕点O至少要旋转考点:旋转的性质
专题:常规题型
分析:根据等边三角形的性质得到点O为等边三角形ABC的中心,则∠AOB=∠AOC=120°,OA=OB=OC,然后根据旋转的定义,可将△AOB绕点O旋转120度后与△AOC重合.
解答:解:∵点O是正三角形ABC三条高的交点,
∴点O为等边三角形ABC的中心,
∴∠AOB=∠BOC=∠AOC=
×360°=120°,OA=OB=OC,
∴△AOB绕点O至少要旋转120度后与△AOC重合.
故答案为:120.
∴点O为等边三角形ABC的中心,
∴∠AOB=∠BOC=∠AOC=
| 1 |
| 3 |
∴△AOB绕点O至少要旋转120度后与△AOC重合.
故答案为:120.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的性质.

练习册系列答案
相关题目
某区共有1万名学生参加数学考试,现从中抽取600名考的数学成绩进行统计分析,以下说法正确的是( )
| A、1万名考生是总体 |
| B、每名考生的数学成绩是个体 |
| C、600名考生是总体的一个样本 |
| D、这是一次成绩普查 |
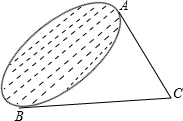 如图,为了求出湖两岸A、B两点间的距离,观测者从测点A、B分别测得∠BAC=90°,∠ABC=30°,又量得BC=160cm,则A、B两点间的距离为
如图,为了求出湖两岸A、B两点间的距离,观测者从测点A、B分别测得∠BAC=90°,∠ABC=30°,又量得BC=160cm,则A、B两点间的距离为