题目内容

若（x+3）2+|2y-6|+（z+2）2=0，则多项式2x-3x+2z-2y-3z+y值等于（　　）
A、0B、3C、1D、2
考点：代数式求值,非负数的性质：绝对值,非负数的性质：偶次方
专题：计算题
分析：利用非负数的性质求出x，y，z的值，代入原式计算即可得到结果．
解答：解：∵（x+3）2+|2y-6|+（z+2）2=0，
∴x=-3，y=3，z=-2，
则原式=-x-y-z=3-3+2=2．
故选D．
点评：此题考查了代数式求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
所有的正数组成正数集合，所有的负数组成负数集合，所有的整数组成整数集合，所有的分数组成分数集合．请把下列各数填入相应的集合中：-2，3.2，0，
2
3
，-1
2
3
，3
负数集合：{
 
…}；整数集合：{
 
…}．
请你写出一个一元二次方程，使得它有一根为正数，另一根为负数：
 
．
3x2y是单项式，它的系数是
 
，次数是
 
．
合并同类项：
①-3x+2x-5x
②2ab2-a2b+5a2b-4ab2
③（a+3b）-（a-b）
④3（m2-2n2）-2（-3n2+m2）
⑤x2-{2xy+[x2-2（xy-y2）]-y2}．
迪雅服装厂生产一种夹克和T恤，夹克每件定价100元，T恤每件定价50元．厂方在开展促销活动期间，向客户提供两种优惠方案：①买一件夹克送一件T恤；②夹克和T恤都按定价的80%付款．现某客户要到该服装厂购买夹克30件，T恤x件（x＞30）．
（1）若该客户按方案①购买，夹克需付款
 
元，T恤需付款
 
元（用含x的式子表示）；若该客户按方案②购买，夹克需付款
 
元，T恤需付款
 
元（用含x的式子表示）；
（2）按方案①购买夹克和T恤共需付款
 
元（用含x的式子表示），方案②购买夹克和T恤共需付款
 
元（用含x的式子表示），购买多少件时两种方案一样？
（3）若两种优惠方案可同时使用，当x=40时，你能给出一种更为省钱的购买方案吗？试写出你的购买方案，并说明理由．
某摩托车厂本周内计划每日生产300辆摩托车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）
星期一二三四五六日
增减-5+7-3+4+10-9-25
（1）本周三生产了多少辆摩托车？
（2）产量最多的一天比产量最少的一天多生产了多少辆？
（3）本周总生产量与计划生产量相比，增加或减少了多少辆？
已知2x3+4x2-8x+3=11，则x3+2x2-4x+8=
 
．
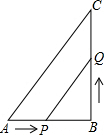在△ABC中，∠B=90°，AB=6cm，BC=12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，设P、Q两点同时出发，移动时间为t秒．
（1）几秒钟后△PBQ是等腰三角形？
（2）几秒钟后△PQB的面积为8cm2？
（3）几秒钟后，以P、B、Q为顶点的三角形和△ABC相似？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网