Question

【题目】对于平面直角坐标系中的点和（半径为），给出如下定义：若点关于点的对称点为，且，则称点为的称心点．

（1）当的半径为2时，

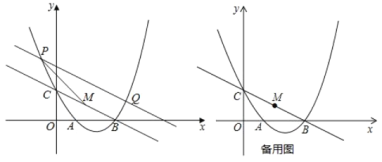
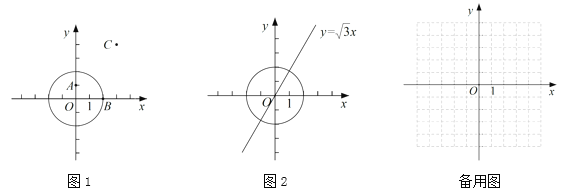
①如图1，在点，，中，的称心点是 ；

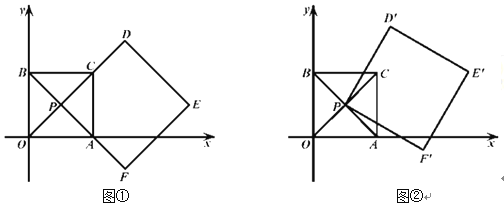
②如图2，点在直线上，若点是的称心点，求点的横坐标的取值范围；

（2）的圆心为，半径为2，直线与轴，轴分别交于点，．若线段上的所有点都是的称心点，直接写出的取值范围．

Answer 1

【答案】（1）①，，②或；（2）或

【解析】

（1）①先求出点A，B，C关于点O的对称点A'，B'，C'进而求出AA'，BB'，CC'，再判断即可得出结论；②先求出点D的坐标，再利用新定义建立不等式求解即可得出结论；

（2）先求出点E，F坐标，进而求出∠EFO=60°，进而找出y轴上到线段EF的距离为2时的位置，再分情况利用新定义，即可得出结论．

解：（1）解：（1）①∵A（0，1），

∴点A关于点O的对称点为A'（0，-1），

∴AA'=1-（-1）=2，

∵⊙O的半径为2，

∴点A是⊙O的称心点，

∵B（2，0），

∴点B关于点O的对称点为B'（-2，0），

∴BB'=2-（-2）=4，

∵⊙O的半径为2，

∴2＜BB'＜6，

∴点B是⊙O的称心点，

∵C（3，4），

∴点C关于点O的对称点为C'（-3，-4），

∴，

∴点C不是的称心点，

故答案为：点A，B；

②如图，设直线与以为圆心，半径为1和3的两个圆的交点从右至左依次为，，，，过点作轴于点,

∵，，

∴，

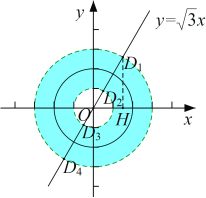
∴点的横坐标为,

同理可求得点，，的横坐标分别为，，．

∴点的横坐标的取值范围是，或．

（2）如图，

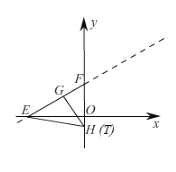
在直线中，

当x=0时，y=1，

∴F（0，1），OF=1，

当时，，

∴E（-，0），OE=，

在Rt△EOF中，，

∴，

过y轴上一点H作直线EF的垂线交线段EF于G，

∵线段EF上的所有点都是⊙T的称心点，且⊙T的半径为2，

∴最小值为1，

在中，，

∴，

∴，

当点T从H向下移动时，GH，FH，EH越来越长，直到点G和E重合，HF取最大值，

∵线段EF上的所有点都是⊙T的称心点，

∴FH=1-t≤3，

∴t≥-2，EH≤3，

∴，

∴，

∴，

当点T从点H向上移动时，点T在FH上时，T到EF的距离小于2，此种情况不符合题意，

当点T从点F向上移动时，ET≥EF，

即：ET≥2，

∵线段EF上的所有点都是⊙T的称心点，

∴FH≥1，EH≤3，

∴，，

∴，

故：的取值范围是，或．