题目内容
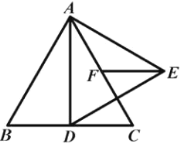
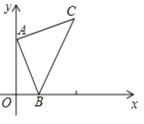
【题目】如图,点![]() 为
为![]() 外一点,点
外一点,点![]() 为
为![]() 上一点,点
上一点,点![]() 为
为![]() 上一点且
上一点且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
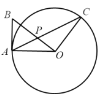
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() 的半径为8.求
的半径为8.求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由等腰三角形的性质可得∠BAP=∠BPA,由![]() ,可证∠C+∠CPO=90°,即可推出∠BAP+∠PAO=90°,结论得证;
,可证∠C+∠CPO=90°,即可推出∠BAP+∠PAO=90°,结论得证;
(2)作BD⊥AP于点D,先求出AB,OP的长,再求出CP长,根据△BPD∽△CPO,得出比例线段,求PD的长,则AP可求.
∵AB=BP,
∴∠BAP=∠BPA,
∵![]() ,
,
∴∠BOC=90°,即∠PCO+∠OPC=90°,
∵OA=OC,
∴∠PAO=∠C,
∵∠BPA=∠CPO,
∴∠BAP+∠PAO=90°,
∴∠BAO=90°,
又∵点![]() 为
为![]() 上一点,
上一点,
∴![]() 是
是![]() 的切线;
的切线;
(2)如图,作BD⊥AP于点D,

在Rt△ABO中,OB=10,OA=8,
则AB=6,OP=4,
在Rt△CPO中,PO=4,CO=8,
则![]() ,
,
∵BA=BP,
∴AD=PD,
∵∠COP=90°,
∵∠BDP=90°,∠BPD=∠CPO,
∴△BPD∽△CPO,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】现今“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

请根据以上信息,解答下列问题:
(1)写出![]() ,
,![]() ,
,![]() ,
,![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)我市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30