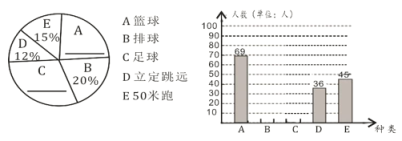
题目内容
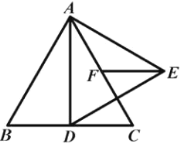
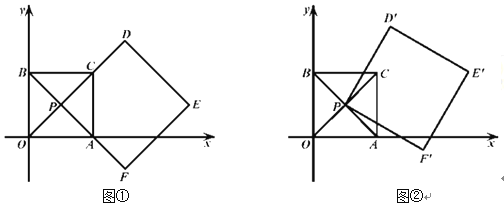
【题目】如图①,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 为正方形
为正方形![]() 对角线的交点,点
对角线的交点,点![]() ,点
,点![]() ,点
,点![]() .分别延长
.分别延长![]() 到
到![]() ,
,![]() 到
到![]() ,使
,使![]() ,
,![]() ,再以
,再以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .
.
(Ⅰ)求点![]() 的坐标;
的坐标;
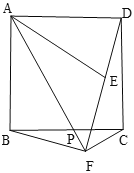
(Ⅱ)如图②,将四边形![]() 绕点
绕点![]() 逆时针旋转得四边形
逆时针旋转得四边形![]() ,点
,点![]() ,
,![]() ,
,![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,
,![]() ,
,![]() ,旋转角为
,旋转角为![]() .
.
①旋转过程中,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在旋转过程中,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
【答案】(Ⅰ)![]() ;(Ⅱ)①
;(Ⅱ)①![]() 或
或![]() ,②
,②![]()
【解析】
(Ⅰ)过![]() 作
作![]() 轴于H,根据四边形
轴于H,根据四边形![]() 是正方形和A、B两点的坐标的得出正方形
是正方形和A、B两点的坐标的得出正方形![]() 的边长为2,再根据正方形的性质得出OP=PC=
的边长为2,再根据正方形的性质得出OP=PC=![]() ,结合已知条件利用三角函数得出OH和DH的长即可.
,结合已知条件利用三角函数得出OH和DH的长即可.
(Ⅱ)①当![]() 时,分旋转角
时,分旋转角![]() =
=![]() 和
和![]() 进行讨论,都是过
进行讨论,都是过![]() 作
作![]() 的垂线,垂足记作
的垂线,垂足记作![]() ,利用等腰三角形的性质和三角函数求得
,利用等腰三角形的性质和三角函数求得![]() 的长,从而确定点
的长,从而确定点![]() 的坐标;
的坐标;
②先根据正方形的判定,结合已知条件证出四边形![]() 是正方形,求出对角线PE=4,从而得出点
是正方形,求出对角线PE=4,从而得出点![]() 的运动轨迹是在以B为圆心,4为半径的圆,继而求出
的运动轨迹是在以B为圆心,4为半径的圆,继而求出![]() 的取值范围;
的取值范围;
解:
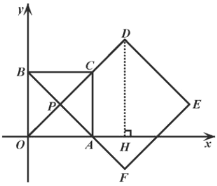
(Ⅰ)过![]() 作
作![]() 轴,垂足记作
轴,垂足记作![]() ,
,
∵四边形![]() 是正方形,
是正方形,![]() ,点
,点![]() ,点
,点![]() .
.
∴正方形![]() 的边长为
的边长为![]() ,
,
∴![]() ,∴
,∴![]()
∵![]() =
=![]() ,∴
,∴![]()
在等腰![]() 中,
中,![]() .
.
∴点![]() 的坐标为
的坐标为![]()
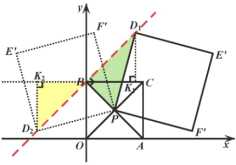
(Ⅱ)①过点![]() 作
作![]() 的垂线
的垂线![]() ,由点
,由点![]() 落在垂线
落在垂线![]() 上.
上.
在![]() 中,
中,
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∴旋转角![]() 或
或![]()
当![]() 时,
时,
在![]() 中,
中,![]()
过![]() 作
作![]() 的垂线,垂足记作
的垂线,垂足记作![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() .
.
∴点![]() 的坐标为
的坐标为![]()
当![]() 时,
时,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
综上所述,当![]() 时点
时点![]() 的坐标为
的坐标为![]() 或
或![]()
②∵四边形![]() 平行四边形,AB⊥OC
平行四边形,AB⊥OC
∴平行四边形![]() 是矩形;
是矩形;
∵![]() ,
,![]() ,PC=PA,
,PC=PA,
∴PD=PF,∴矩形![]() 是正方形;
是正方形;
∴PE=4
∴点![]() 在以B为圆心,4为半径的圆上运动;
在以B为圆心,4为半径的圆上运动;
∴![]() ;
;
∴![]() 的取值范围:
的取值范围:![]()

练习册系列答案
相关题目