题目内容
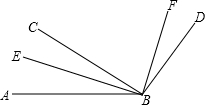如图，∠ABC=60°，∠ABD=145°，BE平分∠ABC．BE⊥BF，求∠FBD的度数．
解：∵∠ABC=60°，BE平分∠ABC，
∴∠COE=
∠ABC=30°，
又∵BE⊥BF，
∴∠CBF=∠EBF-∠EBC=90°-30°=60°，
又∵∠ABD=145°，
∴∠CBD=∠ABD-∠ABC=145°-60°=85°，
∴∠FBD=∠CBD-∠CBF=85°-60°=25°．
故答案为：25°．
分析：根据角平分线的定义，以及已知条件，求出∠COF的度数，进而求出∠FDB的度数．
点评：本题考查了角平分线的定义以及垂直的定义，进而一步步计算，难度适中．
∴∠COE=
∠ABC=30°，又∵BE⊥BF，
∴∠CBF=∠EBF-∠EBC=90°-30°=60°，
又∵∠ABD=145°，
∴∠CBD=∠ABD-∠ABC=145°-60°=85°，
∴∠FBD=∠CBD-∠CBF=85°-60°=25°．
故答案为：25°．
分析：根据角平分线的定义，以及已知条件，求出∠COF的度数，进而求出∠FDB的度数．
点评：本题考查了角平分线的定义以及垂直的定义，进而一步步计算，难度适中．
练习册系列答案
相关题目
5、如图，∠ABC=60°，AD垂直平分线段BC于点D，∠ABC的平分线BE交AD于点E，连接EC，则∠AEC等于（ ）
如图，∠ABC=60°，∠ABD=145°，BE平分∠ABC．BE⊥BF，求∠FBD的度数．
（改编）如图，∠ABC=60°，AD垂直平分线段BC于点D，∠ABC的平分线BE交AD于点E，连接EC，则∠AEC的度数是
21、如图：∠ABC=60°，∠ACB=50°，∠1=∠2，∠3=∠4．