题目内容
 (改编)如图,∠ABC=60°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是
(改编)如图,∠ABC=60°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是分析:根据角平分线的定义可得∠EBD=
∠ABC,再线段垂直平分线上的点到线段两端点的距离相等,BE=CE,根据等边对等角的性质,∠C=∠EBD,利用三角形的一个外角等于与它不相邻的两个内角的和求解.
| 1 |
| 2 |
解答:解:∵∠ABC=60°,∠ABC的平分线BE交AD于点E,
∴∠EBD=
∠ABC=
×60°=30°,
∵点E在BC的垂直平分线上,
∴BE=CE,
∴∠C=∠EBD=30°,
∴∠AEC=∠C+∠EDC=30°+90°=120°.
故答案为:120°.
∴∠EBD=
| 1 |
| 2 |
| 1 |
| 2 |
∵点E在BC的垂直平分线上,
∴BE=CE,
∴∠C=∠EBD=30°,
∴∠AEC=∠C+∠EDC=30°+90°=120°.
故答案为:120°.
点评:本题主要考查了角平分线的定义,线段垂直平分线上的点到线段两端点的距离相等的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,准确识图比较关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 (模拟改编)如图,在△ABC中,∠B=36°,D为BC上的一点,AB=AC=BD=1.
(模拟改编)如图,在△ABC中,∠B=36°,D为BC上的一点,AB=AC=BD=1.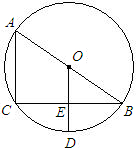 如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编
如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编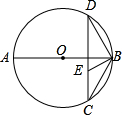 (改编)如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=BE
(改编)如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=BE
